American Journal of Physics, Vol. 72, No. 4, pp. 428–435, April 2004
©2004 American Association of Physics Teachers. All rights reserved.
Symmetries and conservation laws: Consequences of Noether's theorem
Jozef Hanca)
Technical University, Vysokoskolska 4, 042 00 Kosice, Slovakia
Slavomir Tulejab)
Gymnazium arm. gen. L. Svobodu, Komenskeho 4, 066 51 Humenne, Slovakia
Martina Hancovac)
P. J. Safarik University, Jesenna 5, 040 11 Kosice, Slovakia
Received: 30 December 2002; accepted: 23 May 2003We derive conservation laws from symmetry operations using the principle of least action. These derivations, which are examples of Noether's theorem, require only elementary calculus and are suitable for introductory physics. We extend these arguments to the transformation of coordinates due to uniform motion to show that a symmetry argument applies more elegantly to the Lorentz transformation than to the Galilean transformation. © 2004 American Association of Physics Teachers.
Contents
I. INTRODUCTION
"It is increasingly clear that the symmetry group of nature is the deepest thing that we understand about nature today" (Steven Weinberg).1 Many of us have heard statements such as for each symmetry operation there is a corresponding conservation law. The conservation of momentum is related to the homogeneity of space. Invariance under translation in time means that the law of conservation of energy is valid. Such statements come from Noether's theorem, one of the most amazing and useful theorems in physics.
When the German mathematician Emmy Noether proved her theorem,2,3 she uncovered the fundamental justification for conservation laws. This theorem tells us that conservation laws follow from the symmetry properties of nature. Symmetries (called "principles of simplicity" in Ref. 1) can be regarded as a way of stating the most fundamental properties of nature. Symmetries limit the possible forms of new physical laws. The deep connection between symmetry and conservation laws requires the existence of a minimum principle in nature: the principle of least action. In classical mechanics, symmetry arguments are developed using high level mathematics. On the other hand, the corresponding physical ideas often are much easier to understand than the mathematical derivations.
In this paper we give an elementary introduction to the relation between symmetry arguments and conservation laws, as mediated by the principle of least action. We shall use only elementary calculus so that our approach can be used in introductory university physics classes.
Because the paper deals mainly with symmetry, it is important how we define or characterize this concept in the framework of introductory physics. We adopt Feynman's simple description of symmetry from his lectures on physics,4 which says that anything is symmetrical if one can subject it to a certain operation and it appears exactly the same after the operation.
Like Feynman, we will concentrate on symmetry in physical laws. The question is what can be done to a physical law so that this law remains the same. Noether's theorem derives conservation laws from symmetries under the assumption that the principle of least action governs the motion of a particle in classical mechanics. This principle can be phrased as "The action is a minimum for the path (worldline) taken by the particle,"5 which leads to the reformulation of our basic question about symmetry: What changes can we make in the worldline that do not lead to changes in either the magnitude or the form of the action?
We will explore and apply symmetry operations to the action along an infinitesimally small path segment. Because the action is additive, conclusions reached about a path segment apply to the entire path. The simplest examples of symmetry show the independence of the action on the difference in some quantity such as position, time, or angle.6 When such a symmetry exists, Noether's theorem tells us that a physical quantity corresponding to this symmetry is a constant of the motion that does not change along the entire path of the particle.7 The existence of such a constant implies a conservation law, which we then identify.
Section II briefly describes our software that helps students study the action and its connection to conservation laws. Section III analyzes four examples of symmetry operations: translation in space and time, rotation through a fixed angle, and symmetry under uniform linear motion, namely the Galilean transformation. The first three symmetries lead to three conservation laws: momentum, energy, and angular momentum. Section IV extends the analysis to symmetry in relativity, showing that these conservation laws exist in that realm. Moreover, for uniform linear motion the symmetry argument applies more elegantly to the Lorentz transformation than to the Galilean transformation.
In the following we often talk about variations or changes in the action. Consistent with standard practice, we will only be interested in variations representing infinitesimal first-order changes in the action. To keep the arguments simple, we also assume that the particle's invariant mass m (rest mass) does not change during the motion to be studied.
II. SOFTWARE
We start with the well-known definition of action for a particle of mass m that moves from some initial position at time t1 to some final position at time t2:
![<i>S</i> = [integral]<sub><i>t</i><sub>1</sub></sub><sup><i>t</i><sub>2</sub></sup>(KE – PE)<i>d</i><i>t</i>,](symmetry_files/428_1m0.gif)
or equivalently
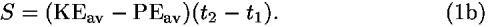
Here KEav denotes the time averaged kinetic energy and PEav the time averaged potential energy between t1 and t2. We use the notation KE and PE as symbols for kinetic and potential energies, respectively, because they are more mnemonic than the traditional symbols T and V.
Action is not a familiar quantity8 for many students, so we employ an interactive computer program9 to help them develop an intuition about the nature of the action and the principle of least action. By using an interactive computer display, the student cannot only explore the operation of the principle of least action, but also study the relation between this principle and conservation laws in specific cases (Fig. 1). In carrying out this manipulation, the student naturally works with the central concepts of a worldline (a graph of the time dependence of a particle's position) and an event (a point on a worldline). Unlike the trajectory in space, the worldline specifies completely the motion of a particle. For background on the symmetry properties of nature, we suggest that our students read a selection from Ref. 10.
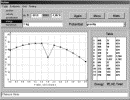 Figure 1.
Figure 1. III. SYMMETRY AND CONSERVATION LAWS IN NEWTONIAN MECHANICS
A. Translation in space
We first examine the symmetry related to translation in space. When we perform an experiment at some location and then repeat the same experiment with identical equipment at another location, then we expect the results of the two experiments to be the same. So the physical laws should be symmetrical with respect to space translation.
As a simple example, consider the action of a free particle (in zero potential or uniform potential) moving along the x axis between two events 1 [t1,x1] and 2 [t2,x2] infinitesimally close to one another along its worldline. Because the worldline section is considered to be straight, the particle moves at constant velocity v = (x2–x1)/(t2–t1) and therefore with a constant kinetic energy (1/2)mv2. According to Eq. (1b), the action along this straight segment in zero potential is (the consideration for uniform potential is analogous)
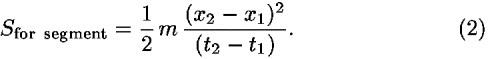
If we change the positions of both observed events by a fixed displacement a, the action remains unchanged (invariant), because the value of the action depends only on the difference between the positions: x2 + a–(x1 + a) = x2–x1. The principle of least action is symmetrical with respect to a fixed displacement of the position. Noether's theorem implies that this symmetry is connected with a conservation law. In the following, we demonstrate that the conservation law related to symmetry under space translation is conservation of momentum.
1. Principle of least action and momentum
Think of the motion of a free particle along the x axis. To explore the connection between the principle of least action and the conservation of momentum, we take advantage of the additive property of the action to require that the action along an arbitrary infinitesimal section of the true worldline have a minimal value.11 Thus we consider three successive infinitesimally close events, 1, 2, and 3 on the particle's worldline and approximate a real worldline by two connected straight segments, A and B (see Fig. 2).
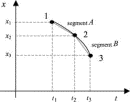 Figure 2.
Figure 2. Because we are considering translation in space, we fix the first and last events, 1 and 3, and change the space coordinate x2 of the middle event 2 so as to minimize the value of the total action S. This minimum condition corresponds to a zero value of the derivative of S with respect to x2:

Because the action is an additive quantity, the total action equals the sum of the actions for segments A and B, so S = S(A) + S(B). If we use Eq. (2), we can write
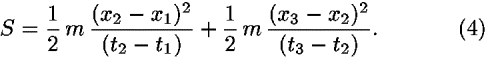
If we perform in Eq. (4) the derivative indicated in Eq. (3), we obtain the condition:
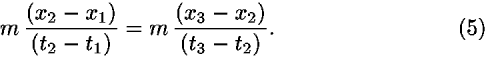
The expression on the left-hand side of Eq. (5) is the momentum pA for segment A while the expression on the right-hand side is the momentum pB for segment B, so pA = pB. We could continue and add other segments C, D, E, to cover the entire worldline that describes the particle motion. For all these segments the momentum will have the same value, which yields the conservation law of momentum. The action for this free particle depends only on the change of the coordinate x and the result of this dependence is the conservation of the particle's momentum.
to cover the entire worldline that describes the particle motion. For all these segments the momentum will have the same value, which yields the conservation law of momentum. The action for this free particle depends only on the change of the coordinate x and the result of this dependence is the conservation of the particle's momentum.
However, this derivation uses only the displacement of one event on the worldline. Therefore, we have not yet demonstrated the relation between the conservation of momentum and the symmetry of translation in space in which all three events are displaced.
2. Symmetry and the conservation of momentum
Now we show the straightforward relation between the symmetry of translation in space and conservation of momentum. Again consider three infinitesimally close events on the worldline x(t) of the free particle shown in Fig. 3 (the extension to the entire worldline will be discussed later).
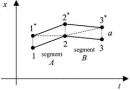 Figure 3.
Figure 3. We shift the worldline x(t) so that every event changes its position by a fixed infinitesimal displacement a. The new events create a shifted worldline which we indicate by an asterisk: x*(t). As pointed out, the form of the action for x*(t) remains unchanged and does not depend on the parameter a. Thus the change in action with respect to the displacement a is zero:
![<i>Delta</i><sub><i>a</i></sub><i>S</i> [equivalent] <i>S</i>(1<sup>*</sup>2<sup>*</sup>3<sup>*</sup>) – <i>S</i>(123) [equivalent] 0.](symmetry_files/428_1m6.gif)
Note that the worldline x*(t) is just as valid as the original one. Therefore the worldline x*(t) also obeys the principle of least action. In translating from x(t) to x*(t) we do not need to shift all the events simultaneously. The same effect is obtained if we first change the position of event 1 (in Fig. 3 only coordinate x1 changes, which creates the worldline 1*23), then event 3 (only x3 changes, which creates 1*23*) and finally event 2 (only x2 changes, which creates 1*2*3*). The total change in action for displacement a can be written as:
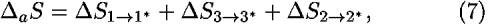
where  S1
S1 1*,
1*,  S2
S2 2*,
2*,  S3
S3 3* denotes the changes in the action after the shifts in the corresponding events.
3* denotes the changes in the action after the shifts in the corresponding events.
Equation (6) tells us that  aS is always zero. The final change
aS is always zero. The final change  S2
S2 2* must also be zero, from the principle of least action applied to the new worldline. Hence Eqs. (6) and (7) give
2* must also be zero, from the principle of least action applied to the new worldline. Hence Eqs. (6) and (7) give

If we now calculate the changes in the action in Eq. (8), we obtain the conservation law of momentum. Because the displacement a is infinitesimal, we can write:
![<i>Delta</i> <i>S</i><sub>1 --> 1<sup>*</sup></sub> [equivalent] <i>S</i>(1<sup>*</sup>23) – <i>S</i>(123) = (<i>d</i><i>S</i>/(<i>d</i><i>x</i><sub>1</sub>)) <i>a</i>,](symmetry_files/428_1m9.gif)
![<i>Delta</i> <i>S</i><sub>3 --> 3<sup>*</sup></sub> [equivalent] <i>S</i>(1<sup>*</sup>23<sup>*</sup>) – <i>S</i>(1<sup>*</sup>23) = (<i>d</i><i>S</i>/(<i>d</i><i>x</i><sub>3</sub>)) <i>a</i>.](symmetry_files/428_1m10.gif)
If we substitute Eq. (9) into Eq. (8) and use the fact that the fixed infinitesimal displacement a is arbitrary, we have12

The application of the derivatives in Eq. (10) to the expression for the action in Eq. (4) yields the identical result for a free particle as Eq. (5), but this time as a result of spatial translation of the entire incremental worldline segment. Thus the left-hand side of Eq. (10) can also be interpreted as the momentum at event 1 and the right-hand side as the momentum at event 3.
The preceding considerations can be applied to the entire worldline x(t). We did not specify the location of the segments A and B. Therefore, an arbitrary number of additional segments can be added between them. Then we shift the segments as before (see Fig. 4). By the same analysis we conclude that the momentum for segment A (effectively the momentum at event 1) has the same value as for segment B (effectively at event 3). The arbitrariness of position of these segments on the worldline means that the value of the momentum remains constant at every event on the worldline. Thus, in classical mechanics, the symmetry of spatial translation means that momentum is conserved for a free particle.
 Figure 4.
Figure 4. The invariance of the action with respect to translation in space is also called the homogeneity of space, which means that all points in space are equivalent. In other words, it does not matter where an experiment is performed. Therefore, we can state that the law of momentum conservation results from the homogeneity of space.
B. Translation in time
It is easy to envision the symmetry related to translation in time. Repeating an experiment on identical initial systems yields the same result when the two experiments are separated by a lapse of time. Our conclusion is that physical laws should not change with translation in time.
Again we will show the relation of translation in time symmetry to a relevant conservation law. We start with an expression for the action of a particle moving in the x direction along an infinitesimally small worldline segment in a potential field described by PE(x). As in Sec. III A the action for this segment can be written according to Eq. (1b) as

where the potential energy is evaluated at the average position along the segment. Now suppose that we translate the time t by an amount 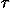 . It is easy to see that the action will not change, because only the difference of the time, t2 +
. It is easy to see that the action will not change, because only the difference of the time, t2 + 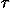 –(t1 +
–(t1 + 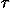 ) = t2–t1, appears in the equation for the action. So the action is symmetrical with respect to a fixed displacement of time t. What conservation law is related to this time symmetry? We will show that it is conservation of energy.
) = t2–t1, appears in the equation for the action. So the action is symmetrical with respect to a fixed displacement of time t. What conservation law is related to this time symmetry? We will show that it is conservation of energy.
We follow the same line of reasoning as for the case of translation in space, but now we fix all position and time coordinates with the exception of t2. Think of a particle that moves along the x axis in the potential field with potential energy PE(x). To simplify the algebra, we denote space and time differences by
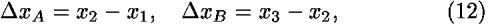
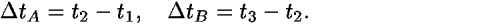
According to Eqs. (11) and (12), the values of the actions S(A) and S(B) for segments A and B are equal to
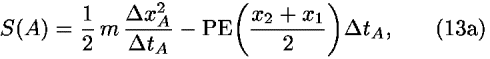
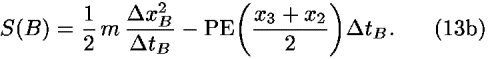
The principle of least action leads to the following condition for the total action S:
![(<i>d</i><i>S</i>/(<i>d</i><i>t</i><sub>2</sub>)) = ((<i>d</i>[<i>S</i>(<i>A</i>) + <i>S</i>(<i>B</i>)])/(<i>d</i><i>t</i><sub>2</sub>)) = 0.](symmetry_files/428_1m17.gif)
If we substitute Eq. (13) into Eq. (14), differentiate, and rearrange the terms, we obtain
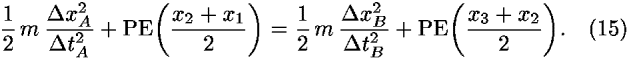
The expressions on both sides of Eq. (15) are sums of average kinetic and potential energies. For infinitesimally close events, Eq. (15) gives an equality for the instantaneous values (1/2)mv + PEA = (1/2)mv
+ PEA = (1/2)mv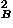 + PEB, and expresses the conservation of mechanical energy.
+ PEB, and expresses the conservation of mechanical energy.
Next we carry out an argument that translates all three times t1, t2, and t3 by the same amount 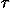 , similar to the way we translated positions for the momentum case. Equations (6,7,8) apply to the present case as well, and also Eq. (9) when the derivatives are taken with respect to time rather than position. Then the result of the temporal translation is an equation similar to Eq. (10):
, similar to the way we translated positions for the momentum case. Equations (6,7,8) apply to the present case as well, and also Eq. (9) when the derivatives are taken with respect to time rather than position. Then the result of the temporal translation is an equation similar to Eq. (10):

which yields Eq. (15) multiplied by (–1). We again obtain conservation of energy, but this time as a result of symmetry under time translation. For infinitesimally close events, the left-hand side of Eq. (16) also can be interpreted as the negative of the total energy at event 1 and the right-hand side as the negative of the energy at event 3. The energy is a constant of the motion for the entire worldline x(t). Similar to the last paragraph of Sec. III A, we can say that the symmetry of translation in time, or in other words the homogeneity of time, implies conservation of energy.
C. Rotation through a fixed angle
We now trace the implications of another symmetry, symmetry under rotation in space. If we rotate an experimental setup through a fixed angle, the experiment will yield the same result. If this symmetry were not true, a laboratory in New York would not be able to verify what is measured in another laboratory in Los Angeles. Indeed, repeating the experiment in New York must lead to the same results as the earth rotates. So physical laws should remain invariant with respect to rotation.
We use polar coordinates to determine which conservation law corresponds to this symmetry and consider the planar motion of a particle in a spherically symmetric potential field of energy PE(r). As before, we consider the expression for the action along the infinitesimal segment. The definition (1b) shows that the action is equal to
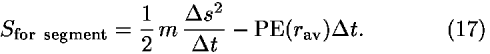
The increment  s is the length of a path segment traveled by the particle during the time interval
s is the length of a path segment traveled by the particle during the time interval  t and rav is the average position of the particle on this segment.
t and rav is the average position of the particle on this segment.
Consider three infinitesimally close points on the real path of a particle and approximate the real path by a broken line consisting of two infinitesimally small segments A and B (Fig. 5). (In this case we do not display a worldline because it would require curves in three-dimensional space–time.) To find the required expression for the action in polar coordinates, we use the Pythagorean theorem. The infinitesimal lengths  sA and
sA and  sB of segments A and B are
sB of segments A and B are

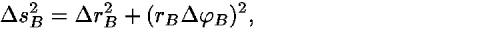
where  rA = r2–r1,
rA = r2–r1, 
 A =
A =  2–
2– 1,
1,  rB = r3–r2, and
rB = r3–r2, and 
 B =
B =  3–
3– 2. If we substitute Eq. (18) into Eq. (17), we find values of the action for segments A, B:
2. If we substitute Eq. (18) into Eq. (17), we find values of the action for segments A, B:
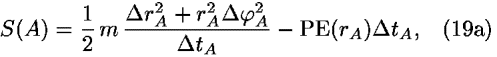
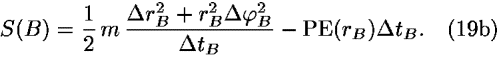
Once again, note that the action for these two segments depends only on the difference in the  coordinate, and not on the
coordinate, and not on the  coordinate itself. As before, we conclude that neither S(A) nor S(B) will change as we increase all
coordinate itself. As before, we conclude that neither S(A) nor S(B) will change as we increase all  coordinates by a fixed angle
coordinates by a fixed angle 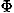 , because
, because  2 +
2 + 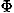 –(
–( 1 +
1 + 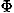 ) =
) =  2–
2– 1. As a result, the motion of the particle is symmetrical with respect to a fixed change in angle
1. As a result, the motion of the particle is symmetrical with respect to a fixed change in angle  . Conservation of angular momentum which arises from this symmetry is derived as follows.
. Conservation of angular momentum which arises from this symmetry is derived as follows.
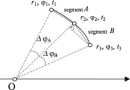 Figure 5.
Figure 5. The condition of stationary action S is expressed as:
![(<i>d</i><i>S</i>/(<i>d</i> <i>phi</i><sub>2</sub>)) = ((<i>d</i>[<i>S</i>(<i>A</i>) + <i>S</i>(<i>B</i>)])/(<i>d</i> <i>phi</i><sub>2</sub>)) = 0.](symmetry_files/428_1m27.gif)
We substitute Eq. (19) into Eq. (20), differentiate and do some rearrangement and obtain:
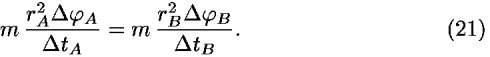
Equation (21) represents conservation of angular momentum L, so LA = LB. The rate of change of the angle is the angular velocity 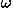 . Thus Eq. (21) can be expressed as mr
. Thus Eq. (21) can be expressed as mr
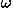 A = mr
A = mr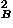
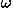 B.
B.
A derivation dealing with the fixed change in the angle coordinate for all three events, similar to those of the previous cases of translations in space and time, yields

which immediately implies conservation of angular momentum (21). Moreover, the left-hand side of Eq. (22) can be interpreted as the angular momentum at point 1 and the right-hand side as the angular momentum at point 3. Angular momentum is conserved for the entire path. The result is that symmetry under rotation through a fixed angle implies conservation of angular momentum.
The condition that physical laws remain invariant with respect to rotation through a fixed angle is called the isotropy of space. That is, space has the same properties in every direction. Therefore conservation of angular momentum results from the isotropy of space.
D. Galilean transformation
Finally, we present a simple example of an interesting and very important symmetry: symmetry under uniform linear motion, known in classical mechanics as Galileo's principle of relativity. We will be surprised to find that the classical action is not invariant under a Galilean transformation.
Consider again a free particle moving along the x axis between closely adjacent events 1 and 2 as observed in a laboratory frame, where the action takes the form (2). The (slowly moving) rocket observer, moving with a velocity vrel with respect to the laboratory, calculates the particle's action given by the same equation
![<i>S</i><sub>for segment</sub><sup>[prime]</sup> = (1/2) <i>m</i> (((<i>x</i><sub>2</sub><sup>[prime]</sup> – <i>x</i><sub>1</sub><sup>[prime]</sup>)<sup>2</sup>)/(<i>t</i><sub>2</sub><sup>[prime]</sup> – <i>t</i><sub>1</sub><sup>[prime]</sup>)).](symmetry_files/428_1m30.gif)
Here we use primes for rocket coordinates, not for the derivative. If we apply the Galilean transformation
![<i>x</i><sup>[prime]</sup> = <i>x</i> – <i>v</i><sub>rel</sub><i>t</i>, <i>t</i><sup>[prime]</sup> = <i>t</i>](symmetry_files/428_1m31.gif)
for the rocket coordinates to Eq. (23), we obtain the following form of the action S![[prime]](symmetry_files/prime-script.gif) in the laboratory frame:
in the laboratory frame:
![<i>S</i><sub>for segment</sub><sup>[prime]</sup> = (1/2) <i>m</i> (((<i>x</i><sub>2</sub> – <i>x</i><sub>1</sub>)<sup>2</sup>)/(<i>t</i><sub>2</sub> – <i>t</i><sub>1</sub>)) – <i>v</i><sub>rel</sub><i>m</i>(<i>x</i><sub>2</sub> – <i>x</i><sub>1</sub>)+(1/2) <i>m</i><i>v</i><sub>rel</sub><sup>2</sup>(<i>t</i><sub>2</sub> – <i>t</i><sub>1</sub>).](symmetry_files/428_1m32.gif)
This form of action is not the same as Eq. (2). The action is not invariant under a Galilean transformation. Which action, S in Eq. (2) or S![[prime]](symmetry_files/prime-script.gif) in Eq. (25), governs the motion of the particle in the laboratory? Or is the Galilean transformation incorrect? According to Appendix A everything is consistent. The two actions S and S
in Eq. (25), governs the motion of the particle in the laboratory? Or is the Galilean transformation incorrect? According to Appendix A everything is consistent. The two actions S and S![[prime]](symmetry_files/prime-script.gif) differ by a function that depends only on the coordinates of a given event, F(x,t) = –vrelmx+
differ by a function that depends only on the coordinates of a given event, F(x,t) = –vrelmx+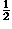 mv
mv t, so the mechanical laws are the same as determined by using S as they are by using S
t, so the mechanical laws are the same as determined by using S as they are by using S![[prime]](symmetry_files/prime-script.gif) .
.
If we use slightly more general considerations, but reasoning similar to that employed previously,13 we can demonstrate that the corresponding conservation law to Galilean transformation (24) is related to the uniform motion of the center of mass.
IV. SYMMETRY AND CONSERVATION LAWS IN RELATIVITY
A. Action in relativity
We have shown that the classical action is not symmetrical with respect to uniform linear motion, but all laws of motion remain unchanged under a Galilean transformation. We believe that this asymmetry for the principle of least action is not accidental, but rather results from the fact that the Galilean transformation and Newton's laws are only approximate laws of motion. Symmetry under uniform linear motion is a basic assumption of Einstein's special relativity.
We consider the same free particle, but now we use the special theory of relativity. The action for linear segment between 1 and 2 has the form:14
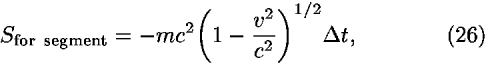
where c is the velocity of light,  t = t1–t2, and v = (x2–x1)/(t2–t1). It can be seen from Eq. (26) that Newtonian mechanics is a special case of relativistic mechanics in the low-velocity limit (v
t = t1–t2, and v = (x2–x1)/(t2–t1). It can be seen from Eq. (26) that Newtonian mechanics is a special case of relativistic mechanics in the low-velocity limit (v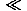 c):
c):
![<i>S</i> [approximate] –<i>m</i><i>c</i><sup>2</sup>(1–(1/2) (<i>v</i><sup>2</sup>/<i>c</i><sup>2</sup>))<i>Delta</i> <i>t</i> = (1/2) <i>m</i><i>v</i><sup>2</sup><i>Delta</i> <i>t</i> – <i>m</i><i>c</i><sup>2</sup><i>Delta</i> <i>t</i>.](symmetry_files/428_1m36.gif)
According to Appendix A, if we take F(x,t) = –mc2t, Eq. (27) will give the same laws of motion for a free particle as the classical Newtonian action in Eq. (2).
B. Lorentz transformation
Now we outline the symmetry argument connected to the relativistic Lorentz transformation which has the form (c = 1):
![<i>x</i> = <i>gamma</i>(<i>x</i><sup>[prime]</sup> + <i>v</i><sub>rel</sub><i>t</i><sup>[prime]</sup>), <i>t</i> = <i>gamma</i>(<i>t</i><sup>[prime]</sup> + <i>v</i><sub>rel</sub><i>x</i><sup>[prime]</sup>),](symmetry_files/428_1m37.gif)
where 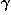 = 1/(1–v
= 1/(1–v )1/2. Here vrel has the same meaning as in Sec. III D. We express the action (26) along a segment of the worldline:
)1/2. Here vrel has the same meaning as in Sec. III D. We express the action (26) along a segment of the worldline:
![<i>S</i><sub>for segment</sub> = –<i>m</i>[(<i>t</i><sub>2</sub> – <i>t</i><sub>1</sub>)<sup>2</sup> – (<i>x</i><sub>2</sub> – <i>x</i><sub>1</sub>)<sup>2</sup>]<sup>1/2</sup>.](symmetry_files/428_1m38.gif)
The expression in the square root is the particle's proper time (wristwatch time) between the two events, which is easily verified to be an invariant under the Lorentz transformation. Hence the relativistic action is symmetrical under a transformation connected to uniform linear motion.
Noether's theorem can be used also in relativity. The same procedure used in Sec. III can be repeated in special relativity to yield the laws of conservation of relativistic energy, momentum, and angular momentum:


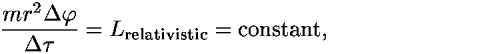
where 
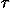 is the particle's proper time. As for the Lorentz transformation, there also exists a corresponding conservation law, but its derivation goes beyond the scope of this paper.15
is the particle's proper time. As for the Lorentz transformation, there also exists a corresponding conservation law, but its derivation goes beyond the scope of this paper.15
We see that the theory of relativity eliminates the asymmetry of the action under translation. The invariance of the action under all the transformations we have considered makes the theory of relativity a more beautiful and elegant theory than the Newtonian theory of classical mechanics.
If one uses the correct expression for the action (or proper time), the constants of motion also can be derived for general relativity without complicated or advanced mathematics.16
V. SUMMARY
We have discussed the connection between symmetries and conservation laws provided by Noether's theorem using only elementary calculus. This approach can be used to help familiarize students with the powerful consequences of symmetry in the physical world. In addition, students can see a unified and systematic approach to all the conservation laws, mediated by Noether's theorem and the principle of least action.
All our considerations can be easily generalized to three dimensions. We note that all symmetries in this paper are one-parameter transformations, which provide the central conservation laws using the most common form of Noether's theorem related to the invariance of the Lagrangian (see Appendix B). Reference 17 and the pedagogically oriented Refs. 18 and 19 give clear, elegant, and more mathematically precise (but much more mathematically oriented) applications of Noether's theorem to particle dynamics.
ACKNOWLEDGMENTS
This paper was written after we read Taylor and Wheeler's general relativity book16 sent to us along with other materials by Taylor, who also made very helpful suggestions for this paper. The authors also wish to thank Nilo C. Bobillo Ares for helpful advice. Slavko Chalupka provided important discussion and encouragement and gave us the opportunity to teach an experimental course in quantum mechanics using some of these ideas.20
APPENDIX A: THE ADDITION OF CERTAIN TERMS TO THE ACTION HAS NO EFFECT ON THE LAWS OF MOTION
Think of two expressions for the action S(12) and S*(12) for a given worldline between any two events 1 and 2 in space–time. Suppose that these two expressions are related to each other as
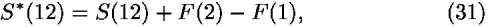
where F is an arbitrary function that depends only on the space and time coordinates of a given event. For example, F(1) could be the value of F at the event 1. Then laws of motion are the same for both forms of action. Why?
We answer this question by repeating the same procedure as for earlier symmetries, starting with three events 1, 2, and 3. If we apply Eq. (31), we obtain the following equations relating action S and S* for segment 1–2 and 2–3:
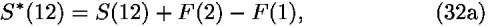
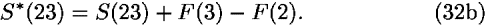
The total action S*(123) is the sum of (32a) and (32b):
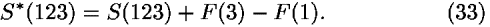
The two total actions S* and S in Eq. (33) differ only in the difference in F at the fixed events 3 and 1. If we change the space or time coordinate (generally u2) of the middle event 2, this difference remains constant. So the minima of S and S* yield the same position of event 2, or in other words, the first derivatives of S and S* with respect to u2 are the same (all other variables being fixed):

According to Eq. (34), the principle of least action for S* gives the same particle's path as in the case of S. The laws of motion are unchanged if an additive constant (the difference in an arbitrary function between final position and initial position of a particle) is added to the action.21
APPENDIX B: NOETHER'S THEOREM AND THE LAGRANGIAN
Noether's theorem determines the connection between constants of the motion and conditions of invariance of the action under different kinds of symmetry. The function KE-PE in Newtonian mechanics is called the Lagrangian and is denoted by the symbol L. So we can write Sfor segment![[equivalent]](symmetry_files/equiv.gif)
 S = L
S = L t. (Do not confuse the symbol L for the action with the symbol L for angular momentum used in Sec. III C.) If we discuss symmetry transformations such that time is transformed identically, t* = t, or transformations involving a uniform time translation, t* = t +
t. (Do not confuse the symbol L for the action with the symbol L for angular momentum used in Sec. III C.) If we discuss symmetry transformations such that time is transformed identically, t* = t, or transformations involving a uniform time translation, t* = t + 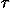 , where
, where  t =
t =  t*, then the invariance of the Lagrangian implies the invariance of the action. Therefore, most textbooks state Noether's theorem as: for each symmetry of the Langrangian, there is a corresponding conserved quantity.
t*, then the invariance of the Lagrangian implies the invariance of the action. Therefore, most textbooks state Noether's theorem as: for each symmetry of the Langrangian, there is a corresponding conserved quantity.
REFERENCES
Citation links [e.g., Phys. Rev. D 40, 2172 (1989)] go to online journal abstracts. Other links (see Reference Information) are available with your current login. Navigation of links may be more efficient using a second browser window.
-
R. P. Feynman and S. Weinberg, Elementary Particles and the Laws of Physics (Cambridge U.P., Cambridge, 1999), p. 73.
first citation in article
-
In reality, there are two Noether's theorems and their converses. The
first one refers to the invariance of the action with respect to a
group of symmetries where the symmetry transformations depend
analytically on many arbitrary finite parameters. The second theorem
deals with the invariance of the action with respect to a group for
which the transformations depend on arbitrary functions and their
derivatives instead of on arbitrary parameters. Our paper considers
one-parameter symmetry transformations. Therefore, it is connected with
the first theorem. See E. Noether, "Invariante Variationsprobleme,"
Nachr. v. d. Ges. d. Wiss. zu Göttingen, Math-phys. Klasse, 235–257
(1918);
English translation by M. A. Tavel, "Invariant variation problem," Transport Theory Stat. Mech.1 (3), 183–207 (1971). Both papers are available at  http://www.physics.ucla.edu/~cwp/Phase2/Noether,_Amalie_Emmy@861234567.html
http://www.physics.ucla.edu/~cwp/Phase2/Noether,_Amalie_Emmy@861234567.html .
first citation in article
.
first citation in article
-
N. Byers, "E. Noether's discovery of the deep connection between
symmetries and conservation laws," Isr. Math. Conf. Proc.12, 67–82 (1999).
first citation in article
-
R. P. Feynman, R. B. Leighton, and M. Sands, The Feynman Lectures on Physics (Addison–Wesley, Reading, MA, 1963), Vol. I, Chap. 11, p. 11-1 or Chap. 52, p. 52-1.
first citation in article
-
More accurately, the principle says that a particle moves along that
path for which the action has a stationary value. So it is frequently
and correctly called the principle of stationary action. See I. M.
Gelfand and S. V. Fomin, Calculus of Variations (Prentice–Hall, Englewood Cliffs, NJ, 1963), Sec. 32.2 or D. J. Morin,
 http://www.courses.fas.harvard.edu/~phys16/handouts/textbook/ch5.pdf
http://www.courses.fas.harvard.edu/~phys16/handouts/textbook/ch5.pdf , Chap. 5.
first citation in article
, Chap. 5.
first citation in article
-
Generally such a quantity is called a cyclic or ignorable coordinate; H. Goldstein, Classical Mechanics (Addison–Wesley, New York, 1970), p. 48 or Ref. 5.
first citation in article
-
Every quantity that depends on position coordinates and velocities and
whose value does not change along actual trajectories is called a
constant of the motion. first citation in article
-
We recommend a more detailed described procedure for introducing action
in J. Hanc, S. Tuleja, and M. Hancova, "Simple derivation of Newtonian
mechanics from the principle of least action," Am. J. Phys. 71, 386–391 (2003). [ISI]
first citation in article
-
The idea of using computers comes from E. F. Taylor. See E. F. Taylor,
S. Vokos, J. M. O'Meara, and N. S. Thornber, "Teaching Feynman's sum
over paths quantum theory," Comput. Phys. 12 (2), 190–199 (1998)
or E. F. Taylor, Demystifying Quantum Mechanics,  http://www.eftaylor.com
http://www.eftaylor.com . Our software is based on Taylor's.
first citation in article
. Our software is based on Taylor's.
first citation in article
-
R. P. Feynman, The Character of Physical Law (Random House, New York, 1994), Chap. 4.
first citation in article
-
Reference 4, Vol. II, Chap. 19, p. 19-8 or the more detailed discussion in Ref. 8.
first citation in article
-
Strictly speaking, in these and the following cases we should use the
more traditional notation of partial instead of total derivatives. But
in all cases it is clear which coordinates are variable and which are
fixed. first citation in article
-
In that case it is necessary to consider the invariance of the action
up to an additive constant (the difference in any arbitrary function
between final position and initial position of a particle), which will
give conservation of motion of the center of mass. See also Refs. 17 or
18. first citation in article
-
The relativistic formula for the action is given in Ref. 4, Vol. II,
Chap. 19. We use the concept of invariance of mass that is used by E.
F. Taylor and J. A. Wheeler, in Spacetime Physics: Introduction to Special Relativity (W. H. Freeman, New York, 1992), 2nd ed.
first citation in article
-
The conservation law corresponding to the Lorentz transformation is derived in L. D. Landau and E. M. Lifshitz, The Classical Theory of Fields (Pergamon, London, 1975), Vol. 2, pp. 41–42.
first citation in article
-
E. F. Taylor and J. A. Wheeler, Exploring Black Holes: An Introduction to General Relativity (Addison–Wesley Longman, New York, 2000), Chaps. 1 and 4; also available at
 http://www.eftaylor.com
http://www.eftaylor.com . The authors use a very similar, easy, and effective variational method.
first citation in article
. The authors use a very similar, easy, and effective variational method.
first citation in article
-
P. Havas and J. Stachel, "Invariances of approximately relativistic Lagrangians and the center of mass theorem. I," Phys. Rev. 185 (5), 1636–1647 (1969). [ISI]
first citation in article
-
N. C. Bobillo-Ares, "Noether's theorem in discrete classical mechanics," Am. J. Phys. 56 (2), 174–177 (1988).
first citation in article
-
C. M. Giordano and A. R. Plastino, "Noether's theorem, rotating potentials, Jacobi's integral of motion," Am. J. Phys. 66 (11), 989–995 (1998).
first citation in article
-
The substance of this article was used by the authors as subjects for
student projects dealing with a special topic on the principle of least
action in a semester quantum mechanics course for future teachers of
physics at the Faculty of Science, P. J. Safarik University, Kosice,
Slovakia. To obtain our materials and corresponding software, see
 http://leastaction.topcities.com
http://leastaction.topcities.com (the mirror site
(the mirror site  http://www.LeastAction.host.sk
http://www.LeastAction.host.sk ) or see Edwin Taylor's website:
) or see Edwin Taylor's website:  http://www.eftaylor.com/leastaction.html
http://www.eftaylor.com/leastaction.html , which also includes our newest, continually updated and expanded materials.
first citation in article
, which also includes our newest, continually updated and expanded materials.
first citation in article
-
L. D. Landau and E. M. Lifshitz, Mechanics (Butterworth–Heinemann, Oxford, 1976), Sec. 1.2.
first citation in article
FIGURES
 Full figure (27 kB)
Full figure (27 kB)Fig. 1. The use of software helps students study the action along a worldline for a particle moving vertically in a gravitational field (as shown) or in other conservative potentials. The user clicks on events to create a worldline and then drags the events to minimize the action, which the computer continuously calculates and displays. The computer also displays a table of energy, momentum, or other quantities that demonstrate conservation of these quantities. Students discover that for the worldline of minimum action, momentum is conserved for the motion of a free particle and that in a gravitational field total energy is conserved. First citation in article
 Full figure (6 kB)
Full figure (6 kB)Fig. 2. Segment of the worldline of a particle that passes through three infinitesimally close events, for which every smooth curve can be approximated by two connected straight segments. First citation in article
 Full figure (5 kB)
Full figure (5 kB)Fig. 3. Three infinitesimally close events 1, 2, 3 on the actual worldline. We shift this worldline through a fixed infinitesimal displacement a. An arbitrary displacement can be composed from a sequence of such infinitesimal displacements. First citation in article
 Full figure (7 kB)
Full figure (7 kB)Fig. 4. Following the same analysis as before, we conclude that the momentum at event 1 is the same as at event 3. The events 1 and 3 can be chosen arbitrarily. The arbitrariness of position of these events on the worldline implies the same value of momentum at every point (event) along the whole worldline of the moving object. First citation in article
 Full figure (6 kB)
Full figure (6 kB)Fig. 5. Path segment of planar motion with three infinitesimally close points whose positions are described by polar coordinates. The radius rA(rB) represents the average position of the particle on segment A(B). All coordinates of the points 1, 2, 3 are fixed with the exception of the angle coordinate  2, which we vary to satisfy the principle of least action. First citation in article
2, which we vary to satisfy the principle of least action. First citation in article
FOOTNOTES
aElectronic mail: jozef.hanc@tuke.sk
bElectronic mail: tuleja@stonline.sk
cElectronic mail: hancova@science.upjs.sk
Up: Issue Table of Contents
Go to: Previous Article | Next Article
Other formats: HTML (smaller files) | PDF (336 kB)
![<i>S</i> = [integral]<sub><i>t</i><sub>1</sub></sub><sup><i>t</i><sub>2</sub></sup>(KE – PE)<i>d</i><i>t</i>,](symmetry_files/428_1m0.gif)
 Figure 1.
Figure 1.  Figure 2.
Figure 2. 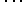 to cover the entire worldline that describes the particle motion. For all these segments the momentum will have the same value, which yields the conservation law of momentum. The action for this free particle depends only on the change of the coordinate x and the result of this dependence is the conservation of the particle's momentum.
to cover the entire worldline that describes the particle motion. For all these segments the momentum will have the same value, which yields the conservation law of momentum. The action for this free particle depends only on the change of the coordinate x and the result of this dependence is the conservation of the particle's momentum.  Figure 3.
Figure 3.  S1
S1 1*,
1*,  S2
S2 2*,
2*,  S3
S3 3* denotes the changes in the action after the shifts in the corresponding events.
3* denotes the changes in the action after the shifts in the corresponding events.  aS is always zero. The final change
aS is always zero. The final change  S2
S2 2* must also be zero, from the principle of least action applied to the new worldline. Hence Eqs. (6) and (7) give
2* must also be zero, from the principle of least action applied to the new worldline. Hence Eqs. (6) and (7) give  Figure 4.
Figure 4. 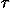 . It is easy to see that the action will not change, because only the difference of the time, t2 +
. It is easy to see that the action will not change, because only the difference of the time, t2 + 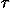 –(t1 +
–(t1 + 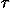 ) = t2–t1, appears in the equation for the action. So the action is symmetrical with respect to a fixed displacement of time t. What conservation law is related to this time symmetry? We will show that it is conservation of energy.
) = t2–t1, appears in the equation for the action. So the action is symmetrical with respect to a fixed displacement of time t. What conservation law is related to this time symmetry? We will show that it is conservation of energy. 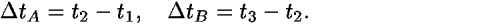
 + PEA = (1/2)mv
+ PEA = (1/2)mv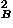 + PEB, and expresses the conservation of mechanical energy.
+ PEB, and expresses the conservation of mechanical energy. 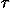 , similar to the way we translated positions for the momentum case. Equations (6,7,8) apply to the present case as well, and also Eq. (9) when the derivatives are taken with respect to time rather than position. Then the result of the temporal translation is an equation similar to Eq. (10):
, similar to the way we translated positions for the momentum case. Equations (6,7,8) apply to the present case as well, and also Eq. (9) when the derivatives are taken with respect to time rather than position. Then the result of the temporal translation is an equation similar to Eq. (10):  s is the length of a path segment traveled by the particle during the time interval
s is the length of a path segment traveled by the particle during the time interval  t and rav is the average position of the particle on this segment.
t and rav is the average position of the particle on this segment.  sA and
sA and  sB of segments A and B are
sB of segments A and B are 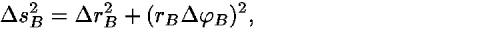
 rA = r2–r1,
rA = r2–r1, 
 A =
A =  2–
2– 1,
1,  rB = r3–r2, and
rB = r3–r2, and 
 B =
B =  3–
3– 2. If we substitute Eq. (18) into Eq. (17), we find values of the action for segments A, B:
2. If we substitute Eq. (18) into Eq. (17), we find values of the action for segments A, B:  coordinate, and not on the
coordinate, and not on the  coordinate itself. As before, we conclude that neither S(A) nor S(B) will change as we increase all
coordinate itself. As before, we conclude that neither S(A) nor S(B) will change as we increase all  coordinates by a fixed angle
coordinates by a fixed angle 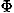 , because
, because  2 +
2 + 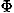 –(
–( 1 +
1 + 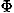 ) =
) =  2–
2– 1. As a result, the motion of the particle is symmetrical with respect to a fixed change in angle
1. As a result, the motion of the particle is symmetrical with respect to a fixed change in angle  . Conservation of angular momentum which arises from this symmetry is derived as follows.
. Conservation of angular momentum which arises from this symmetry is derived as follows.  Figure 5.
Figure 5. 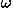 . Thus Eq. (21) can be expressed as mr
. Thus Eq. (21) can be expressed as mr
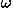 A = mr
A = mr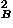
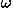 B.
B. ![[prime]](symmetry_files/prime-script.gif) in the laboratory frame:
in the laboratory frame: ![[prime]](symmetry_files/prime-script.gif) in Eq. (25), governs the motion of the particle in the laboratory? Or is the Galilean transformation incorrect? According to Appendix A everything is consistent. The two actions S and S
in Eq. (25), governs the motion of the particle in the laboratory? Or is the Galilean transformation incorrect? According to Appendix A everything is consistent. The two actions S and S![[prime]](symmetry_files/prime-script.gif) differ by a function that depends only on the coordinates of a given event, F(x,t) = –vrelmx+
differ by a function that depends only on the coordinates of a given event, F(x,t) = –vrelmx+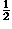 mv
mv t, so the mechanical laws are the same as determined by using S as they are by using S
t, so the mechanical laws are the same as determined by using S as they are by using S![[prime]](symmetry_files/prime-script.gif) .
.  t = t1–t2, and v = (x2–x1)/(t2–t1). It can be seen from Eq. (26) that Newtonian mechanics is a special case of relativistic mechanics in the low-velocity limit (v
t = t1–t2, and v = (x2–x1)/(t2–t1). It can be seen from Eq. (26) that Newtonian mechanics is a special case of relativistic mechanics in the low-velocity limit (v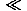 c):
c): 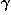 = 1/(1–v
= 1/(1–v )1/2. Here vrel has the same meaning as in Sec. III D. We express the action (26) along a segment of the worldline:
)1/2. Here vrel has the same meaning as in Sec. III D. We express the action (26) along a segment of the worldline: 
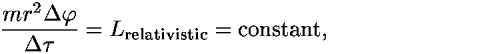

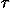 is the particle's proper time. As for the Lorentz transformation, there also exists a corresponding conservation law, but its derivation goes beyond the scope of this paper.15
is the particle's proper time. As for the Lorentz transformation, there also exists a corresponding conservation law, but its derivation goes beyond the scope of this paper.15 ![[equivalent]](symmetry_files/equiv.gif)
 S = L
S = L t. (Do not confuse the symbol L for the action with the symbol L for angular momentum used in Sec. III C.) If we discuss symmetry transformations such that time is transformed identically, t* = t, or transformations involving a uniform time translation, t* = t +
t. (Do not confuse the symbol L for the action with the symbol L for angular momentum used in Sec. III C.) If we discuss symmetry transformations such that time is transformed identically, t* = t, or transformations involving a uniform time translation, t* = t + 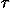 , where
, where  t =
t =  t*, then the invariance of the Lagrangian implies the invariance of the action. Therefore, most textbooks state Noether's theorem as: for each symmetry of the Langrangian, there is a corresponding conserved quantity.
t*, then the invariance of the Lagrangian implies the invariance of the action. Therefore, most textbooks state Noether's theorem as: for each symmetry of the Langrangian, there is a corresponding conserved quantity.  http://www.physics.ucla.edu/~cwp/Phase2/Noether,_Amalie_Emmy@861234567.html
http://www.physics.ucla.edu/~cwp/Phase2/Noether,_Amalie_Emmy@861234567.html .
first citation in article
.
first citation in article  http://www.courses.fas.harvard.edu/~phys16/handouts/textbook/ch5.pdf
http://www.courses.fas.harvard.edu/~phys16/handouts/textbook/ch5.pdf , Chap. 5.
first citation in article
, Chap. 5.
first citation in article  http://www.eftaylor.com
http://www.eftaylor.com . Our software is based on Taylor's.
first citation in article
. Our software is based on Taylor's.
first citation in article  http://www.eftaylor.com
http://www.eftaylor.com . The authors use a very similar, easy, and effective variational method.
first citation in article
. The authors use a very similar, easy, and effective variational method.
first citation in article  http://leastaction.topcities.com
http://leastaction.topcities.com (the mirror site
(the mirror site  http://www.LeastAction.host.sk
http://www.LeastAction.host.sk ) or see Edwin Taylor's website:
) or see Edwin Taylor's website:  http://www.eftaylor.com/leastaction.html
http://www.eftaylor.com/leastaction.html , which also includes our newest, continually updated and expanded materials.
first citation in article
, which also includes our newest, continually updated and expanded materials.
first citation in article  Full figure (27 kB)
Full figure (27 kB) Full figure (6 kB)
Full figure (6 kB) Full figure (5 kB)
Full figure (5 kB) Full figure (7 kB)
Full figure (7 kB) Full figure (6 kB)
Full figure (6 kB) 2, which we vary to satisfy the principle of least action. First citation in article
2, which we vary to satisfy the principle of least action. First citation in article