American Journal of Physics, Vol. 71, No. 4, pp. 386–391, April 2003
©2003 American Association of Physics Teachers. All rights reserved.
Simple derivation of Newtonian mechanics from the principle of least action
Jozef Hanca)
Technical University, Vysokoskolska 4, 042 00 Kosice, Slovakia
Slavomir Tulejab)
P. J. Safarik University, Moyzesova 16, 041 54 Kosice, Slovakia
Martina Hancovac)
P. J. Safarik University, Jesenna 5, 040 11 Kosice, Slovakia
Received: 13 May 2002; accepted: 23 October 2002We present a method for introducing students to the classical principle of least action, using a novel approach based on the ordinary calculus of one variable. We define the classical action for a path and draw the connection between it and Newton's laws for a free particle and for a particle in a conservative potential. The use of software to help students visualize the principle of least action and analyze rectilinear motion is discussed. We also briefly discuss the origin of the principle of least action in Feynman's sum over paths formulation of quantum mechanics. © 2003 American Association of Physics Teachers.
Contents
I. INTRODUCTION
Since Newton's time, classical mechanics has been elegantly reformulated as a single unifying principle known as Hamilton's principle. Following Feynman1 and Landau,2 Hamilton's principle is frequently called "the principle of least action." According to the least action formulation of classical mechanics, a particle moves along the path for which the action (symbolized by S) is a minimum. In some cases the true path does not yield a minimum for S but an inflection point or, in general, a stationary value. Hence a more accurate name for this principle is the principle of stationary action.3
A clear and interesting introduction to the principle of least action can be found in Ref. 1. How are we to find the path of least action? This is a difficult problem belonging to the calculus of variations. We will describe one way around this complicated mathematics which we believe provides a deep understanding of the principle of least action for beginning students. The key idea is based on a passage from Feynman's lectures,4 where he mentions that if the action S is minimum along the true path, then it is also a minimum along every subsection of the path.
To explain the meaning of Feynman's statement, we will consider motion in only one space dimension and plot the actual particle's motion in space and time, xA(t), a plot called a worldline. The principle of least action says that the worldline xA(t) yields a minimal action. Now choose an arbitrary subsection A of this worldline. Draw a nearby worldline xB(t) that differs from xA(t) only on the section A, where xB(t) creates a new section B (see Fig. 1). As we will see in Sec. III A, the total action for a worldline can be expressed as a sum of actions for each of its sections. The value of the action is identical along common sections of both worldlines xA(t) and xB(t). Therefore, the difference in the total action between xA(t) and xB(t) is due to different contributions to the action from sections A and B. In order to not violate the condition of minimal total action, the action for section B must be greater than action for the section A. But the location of subsection A along the worldline was chosen arbitrarily. Therefore, we require that the worldline with minimal action must also satisfy the principle of least action between any pair of intermediary points. Consequently, the principle for the entire path can be stated in Feynman's infinitesimal form:4 the action along an arbitrary infinitesimal section of the true worldline has a minimal value. For an infinitesimal section it is unimportant how the potential varies from one place to another place far away; only the local first-order change in the potential is important. So the result can depend only on the derivative of the potential that is the force at a point.4
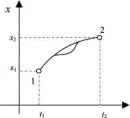 Figure 1.
Figure 1. If we proceed from this formulation (due to Feynman) of the principle for an infinitesimal section of the path, we see that the principle of least action leads to Newton's second law, and only ordinary calculus is needed to derive almost all of classical mechanics.5
In Sec. II we illustrate some of the features of our software which we use as a pedagogical tool for introducing the least action formulation of classical mechanics. In Sec. III we use the definition of the classical action to relate it to Newton's laws in two cases: the motion of a free particle and a particle in a conservative potential field. Our variational method requires only ordinary derivatives. Section IV briefly describes the meaning of action in quantum mechanics and the origin of the classical principle of least action in Feynman's sum over paths formulation of quantum mechanics.
Traditionally the principle of least action is taught in advanced classical mechanics courses. However, the method described in this paper has allowed us to teach it as early as secondary school. We include three pedagogical notes on teaching strategies derived from our use of the principle of least action with classes at both the secondary school and university levels.6
II. INTRODUCTION TO THE PRINCIPLE OF LEAST ACTION
Feynman7 tells us that there are two natural ways to find the path that satisfies the principle of least action. One is the trial-and-error method. We calculate the action for millions of paths and find the one that has the smallest value of the action. Because this method is straightforward but tedious, we turn it over to a computer.8 Using a computer also can help students to visualize and develop an intuition for the process. Such a computer program is illustrated in Fig. 2. In manipulating this program, the student naturally becomes accustomed to the central concepts of worldline (a plot of the particle's position as a function of time) and event (a point on the worldline). With almost no mathematical formalism the student can explore the motion of a particle in various potentials by comparing the action along the true worldline with that along alternative worldlines. For the worldline of least action the result is the same as that derived from Newton's laws. On the display the student can see the numerical values of the action and the following mechanical quantities on the particle's path: position, velocity, acceleration, momentum, and energy.
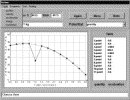 Figure 2.
Figure 2. The second way to find the path that satisfies the principle of least action is mathematical. In contrast to the trial-and-error method, mathematics allows us to include all possible paths and to prove that the path minimizing action S is the one that obeys Newton's laws.
III. PRINCIPLE OF LEAST ACTION AND NEWTON'S LAWS
A. Definition of action and some special cases
Consider a particle of mass m that starts from some fixed initial position at time t1 and moves to a fixed final position at a later time t2. The general expression for the action along the particle's trajectory is
![<i>S</i> [equivalent] [integral]<sub><i>t</i><sub>1</sub></sub><sup><i>t</i><sub>2</sub></sup>(KE – PE)d<i>t</i>.](newton_mechanics_files/386_1m0.gif)
We use unconventional double letters KE and PE as symbols for the kinetic and potential energies, respectively, because they are more mnemonic than the usual symbols T and V. Equation (1a) can be written in the form
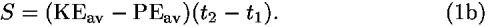
The average energies, KEav and PEav, are given by integrals similar to that in Eq. (1a) divided by (t2–t1). Each of these averages is a function (or more exactly a functional) of the worldline taken by the particle. Equation (1b) can be rewritten in many convenient ways, depending on the nature of the analysis.
(1) If the worldline is straight, then the particle moves at a constant velocity and therefore with a constant kinetic energy KE. In this case the action has the form
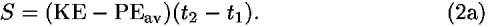
(2) If, in addition, the potential energy is a linear function along the straight worldline, then the average value of PE equals the value of PE at the midpoint of the path. In this case
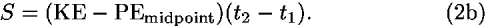
(3) Equation (1b) is valid for any increment of a particle's worldline:
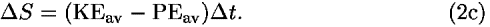
(4) For a very small (or infinitesimal) increment of the worldline (therefore taken to be straight), we can again use Eq. (2b):
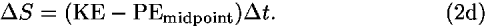
(5) As we see from Eq. (1a), the action for an infinitesimal segment of worldline can be expressed as

Equation (1b) leads to the same conclusion, because for an infinitesimal segment of a worldline, the average energies can be substituted for the instantaneous energies. Equations (1a) and (1b) embody the fact that the action is an additive quantity.
Pedagogical note 1: From the mathematical point of view, the definitions (1a) and (1b) are equivalent, as can be shown by using the integral definition of the average value for a function. But psychologically they are quite different, especially for students new to calculus. In our experience students find the nonintegral definition more acceptable. Another advantage of beginning with Eq. (1b) is that students already are aware of similar average quantities from kinematics.
Expressions for the averages used in the action formula (1b) do not require the solution of integrals in simple cases [see Eqs. (2a) and (2b)]. Because the integral is the same as the area under a curve, elementary methods for the calculation of average values are sufficient, quick, and easy. This connection between the integral and the area also provides a natural way to pass from definition (1b) to the integral (1a). [End of the pedagogical note 1.]
B. Free particles
First we look at the predictions of the principle of least action for free particles in a zero (or constant) potential. Newton's first law of motion tells us that the free object moves along a straight worldline. So our first task is to solve the following problem.
Problem 1. From the principle of least action, show that a free particle that starts from some position at time t1 (event 1) and arrives at a different position at time t2 (event 2), moves along a straight worldline.
Solution: Consider only motion in one dimension. (It is not difficult to generalize to higher dimensions.) Figure 3 shows some of the infinite number of worldlines that can connect events 1 and 2. Which worldline is the one actually followed by the particle?
 Figure 3.
Figure 3. Consider any smoothly curved worldline that is different from a straight worldline between two events. We can approximate this worldline by a series of straight-line segments that create a broken but continuous worldline. The number of these segments can be arbitrary. Denote this number by n. As will be seen, for the case of a broken worldline, it is easy to show by induction that the smallest value of the action belongs to a straight worldline between the two events. Because the smooth worldline can be considered as a limiting case of straight-line segment approximation as n approaches infinity and the validity of the least action statement does not change as n increases without limit, the action for the smooth worldline will always be greater than the action along the straight worldline.
To take the first step of proof by induction, demonstrate the triangle inequality for action on any broken worldline. Consider three events 1, 2, 3 connected by a broken worldline connecting points 1, 2, 3 that are not collinear. Without loss of generality we can take events with equally spaced times t1, t2, t3. (The analysis is the same for events not equally spaced in time, but is less transparent because it requires more subscripts.) In particular we want to prove that S(13)<S(12) + S(23), where contributions to the action S(13), S(12), and S(23) correspond to the path segments 13, 12, and 23 respectively. Consider the sum S(12) + S(23), which is equal to the total action Stotal for the broken line 123 and recall that the action is additive. From Eq. (2a) and the classical expression for the kinetic energy, we have
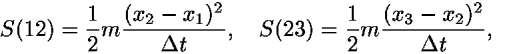
and
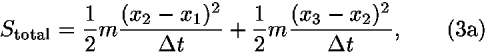
where xi denotes the positions of event i (i = 1,2,3), and 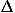 t is the difference between the corresponding times.
t is the difference between the corresponding times.
We assume a nonzero spatially uniform potential energy PE. Then PEav equals PE and according to Eq. (2a), corresponding actions have the form
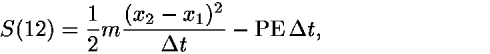
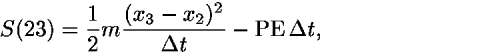
and

If only x2 is variable, then the sum in both cases is a quadratic function of x2 with a positive coefficient. (It is easy to verify this property by multiplying out the expression.) In this case the parabola has a vertex that describes the minimum of the function.
If we take the derivative of Eq. (3a) with respect to x2, the result is
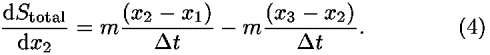
Note that we also obtain Eq. (4) for the derivative in a nonzero spatially uniform potential, because the derivative of the additional term in the action in Eq. (3b) corresponding to constant potential energy has zero value.
If we set the right-hand side in Eq. (4) equal to zero to find the minimum of the sum, we obtain9
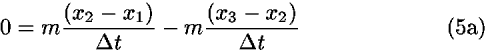
or
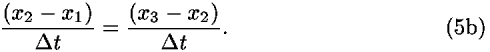
Equation (5b) tells us that the slopes of the two segments have to be equal, which is true only for a straight line. Therefore events 1, 2, and 3 lie on a straight worldline, which also implies the law of conservation of momentum. So for both zero potential and uniform potential, every broken worldline has a greater value of the action than the value corresponding to a straight worldline connecting the same two end events. By induction (see Fig. 4) the same result holds for any worldline composed of n straight-line segments, and in the limit as n
![[infinity]](newton_mechanics_files/infin.gif) , it holds for any continuous smooth worldline. The action has the smallest value for a straight worldline connecting the events, that is, the motion corresponds to constant velocity.
, it holds for any continuous smooth worldline. The action has the smallest value for a straight worldline connecting the events, that is, the motion corresponds to constant velocity.
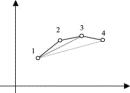 Figure 4.
Figure 4. Pedagogical note 2: It is helpful to have students first consider the simplest possible case of the motion of a free object in zero potential, namely, one in which the space coordinates of the initial and final events are the same (x1 = x2). In this case the straight worldline with constant x coordinate in the space–time diagram yields the value zero for the action S(12). Definition (1b) for the action shows that the action is always non-negative, because the kinetic energy is a non-negative quadratic function at every point on the worldline so its average value in the expression for the action must be a non-negative number. Therefore, an arbitrary worldline connecting events 1 and 2 will have an action greater than zero unless it is the straight worldline connecting the two points. Consequently, the principle of least action tells us that the particle remains at rest at the same point in space between the initial and final events. This demonstration avoids calculus completely. [End of the pedagogical note 2.]
C. Newton's second law
When the potential energy varies with position, we can show that the path with minimal action satisfies Newton's second law for forces derivable from a conservative potential. In the following10 we apply Feynman's formulation of the principle of least action for the infinitesimal path segments mentioned in Sec. I.
Consider an object moving in a potential energy field PE(x). Choose three events 1, 2, 3 that are infinitesimally close together on its worldline, as shown in Fig. 5; these events approximate the real-worldline segment by a once-broken line and represent a little section of a real worldline that is initially unknown. Label A the segment between 1 and 2 and B the segment between 2 and 3. Let x1, x2, x3 be the spatial coordinates of these events and t1, t2, t3 be the corresponding times. Now use the principle of least action to find the true worldline representing real motion between 1 and 3.
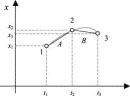 Figure 5.
Figure 5. To start, fix all times and positions with the exception of x2. Then vary the position of x2 to minimize the action for the once-broken path. To simplify the algebra, use equal time intervals denoted by 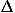 t:
t:

The small loss in generality involved in equal time intervals can be removed easily (see pedagogical note 3).
As in Sec. III A, especially from Eqs. (2d) and (6), we obtain contributions to the action for segments A and B:
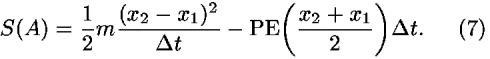
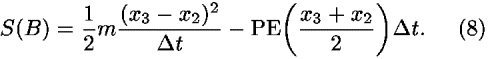
Now we have to find the value of x2 that minimizes the total action Stotal:
![((d<i>S</i><sub>total</sub>)/(d<i>x</i><sub>2</sub>)) = ((d[<i>S</i>(<i>A</i>) + <i>S</i>(<i>B</i>)])/(d<i>x</i><sub>2</sub>)) = 0.](newton_mechanics_files/386_1m18.gif)
After taking the derivatives dS(A)/dx2 and dS(B)/dx2, we obtain

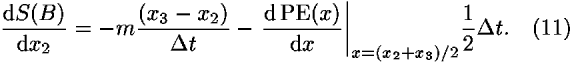
Because events 1, 2, 3 are close to one another, we can write for the derivatives
![((d PE(<i>x</i>))/(d<i>x</i>))|<sub><i>x</i> = (<i>x</i><sub>1</sub> + <i>x</i><sub>2</sub>)/2</sub> [approximate] ((d PE(<i>x</i>))/(d<i>x</i>))|<sub><i>x</i> = <i>x</i><sub>2</sub></sub> [approximate] ((d PE(<i>x</i>))/(d<i>x</i>))|<sub><i>x</i> = (<i>x</i><sub>2</sub> + <i>x</i><sub>3</sub>)/2</sub>.](newton_mechanics_files/386_1m21.gif)
If we substitute Eqs. (12), (10), and (11) into Eq. (9), we arrive at the condition for the minimal action,
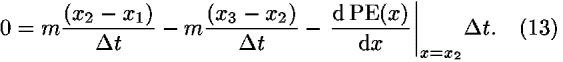
After some rearrangements, we obtain
![–((d PE(<i>x</i>))/(d<i>x</i>))|<sub><i>x</i><sub>2</sub></sub> = <i>m</i>[(((<i>x</i><sub>3</sub> – <i>x</i><sub>2</sub>))/(<i>Delta</i> <i>t</i>))–(((<i>x</i><sub>2</sub> – <i>x</i><sub>1</sub>))/(<i>Delta</i> <i>t</i>))]/<i>Delta</i> <i>t</i>](newton_mechanics_files/386_1m23.gif)
or
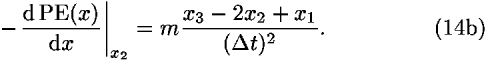
On the left-hand side of Eq. (14) is the well-known expression, the negative derivative of the potential energy for a force F acting on a particle at point 2 in the potential field. The right-hand side of Eq. (14b) divided by m is simply the three-point formula for the second derivative of x with respect to t.11 In the limit of infinitesimal 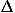 t, this term gives the instantaneous acceleration a at the point 2. Hence, we obtain
t, this term gives the instantaneous acceleration a at the point 2. Hence, we obtain

We could continue and add other segments C,D,E, so that we would cover the entire worldline that describes the motion of the particle. For each of these segments the outcome yields the same Eq. (15). So we have found the connection between the principle of least action and Newton's second law. The worldline representing the path with minimal (stationary) action is the one satisfying Newton's law.
so that we would cover the entire worldline that describes the motion of the particle. For each of these segments the outcome yields the same Eq. (15). So we have found the connection between the principle of least action and Newton's second law. The worldline representing the path with minimal (stationary) action is the one satisfying Newton's law.
Following Feynman,1 we remark on some other generalizations. Consider a situation in which a particle in a potential field moves on an arbitrary path 1–2–3 in three-dimensional space. Each translation in space can be analyzed as an independent translation in one of the three dimensions. Therefore, we can think of carrying out independent translations in the x, y, and z directions, thus arriving at the resulting three equations represent the component notation of one vector equation: Fx = max, Fy = may, Fz = maz or the vector equation

Equation (16) is the general expression for Newton's second law. Using a similar procedure, we can also generalize to the case of many particles.1
Pedagogical note 3: The preceding general variational method is a bit difficult for students. It is sufficient if students are introduced to the result using a special case of the potential field, such as the earth's gravitational field, for which the potential function is linear in one space dimension. In that case the above procedure is more understandable and much more straightforward. Moreover, the case of a linear potential energy function leads to only a quadratic function, which again allows us to use a noncalculus derivation.9
The right-hand side of Eq. (14a) can be explained to students without knowledge of the three-point formula for the second derivative. We identify the two terms in the numerator on the right-hand side of Eq. (14a) as the average velocities on segments A and B. In other words, these velocities are the values at the midpoints of line segments A and B. Because the estimated change in velocity takes just the time 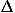 t, the time between the midpoints of the segments, the rate in Eq. (14a) represents the average acceleration.
t, the time between the midpoints of the segments, the rate in Eq. (14a) represents the average acceleration.
Our software (see Fig. 2) calculates the acceleration at any point of the broken worldline according to a more general formula that involves unequal times 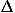 tA and
tA and 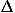 tB for segments A and B,
tB for segments A and B,
![<i>a</i> = [(((<i>x</i><sub>3</sub> – <i>x</i><sub>2</sub>))/(<i>Delta</i> <i>t</i><sub><i>B</i></sub>))–(((<i>x</i><sub>2</sub> – <i>x</i><sub>1</sub>))/(<i>Delta</i> <i>t</i><sub><i>A</i></sub>))]/[((<i>Delta</i> <i>t</i><sub><i>A</i></sub>)/2)+((<i>Delta</i> <i>t</i><sub><i>B</i></sub>)/2)].](newton_mechanics_files/386_1m27.gif)
Equation (17) leads to the derivation of Newton's second law in a way closely similar to the case of equal time lapses. The numerator of Eq. (17) is again the change in velocity, and the denominator is the time between the midpoints of the segments. Students can use this fact to generalize the acceleration formulas (14a)–(17) without needing to derive Newton's second law for unequal time intervals. [End of the pedagogical note 3.]
IV. PRINCIPLE OF LEAST ACTION: WHERE DOES IT COME FROM?
The principle of least action says that a particle moves on the path for which the action S is a stationary. After deriving Newton's laws from the principle of least action, then, according to Feynman, some questions naturally arise: What is the origin of the principle of least action? How does the particle find the right path (or worldline)? Does it "smell" the neighboring paths to find out whether or not they have increased action?1
Newtonian mechanics cannot answer these questions. Indeed, the principle of least action has a deep explanation in quantum mechanics. There are three apparently different mathematical formulations of nonrelativistic quantum mechanics due to Schrödinger, Heisenberg, and Feynman. The last one provides a simple justification of a minimum principle that is very accessible to students.
We recapitulate briefly the basic ideas of Feynman's formulation of quantum mechanics.12 According to this formulation, the particle explores all possible paths between fixed initial and final events. The action along these many paths plays a fundamental role. As Feynman says:13 "The complete quantum mechanics works as follows: The probability that a particle starting at point 1 at the time t1 will arrive at point 2 at time t2 is the square of probability amplitude. The total amplitude can be written as the sum of the amplitudes for each possible path [worldline] for each way of arrival. For every x(t)
works as follows: The probability that a particle starting at point 1 at the time t1 will arrive at point 2 at time t2 is the square of probability amplitude. The total amplitude can be written as the sum of the amplitudes for each possible path [worldline] for each way of arrival. For every x(t) we have to calculate an amplitude. Then we add them all together. The amplitude is proportional to some constant times exp(iS/
we have to calculate an amplitude. Then we add them all together. The amplitude is proportional to some constant times exp(iS/![[h-bar]](newton_mechanics_files/planck.gif) ), where S is action for that path."
), where S is action for that path."
It is the magnitude of S that leads to a seamless transition between classical and quantum mechanics. If S is very large compared to Planck's constant ![[h-bar]](newton_mechanics_files/planck.gif) (as is the typical situation for systems described successfully by classical mechanics), we can say roughly that the amplitudes for all paths have very different phases and cancel out in taking the sum, except for those that are extremely close to the path with minimal action. So in the classical limit,
(as is the typical situation for systems described successfully by classical mechanics), we can say roughly that the amplitudes for all paths have very different phases and cancel out in taking the sum, except for those that are extremely close to the path with minimal action. So in the classical limit, ![[h-bar]](newton_mechanics_files/planck.gif)
 0, the quantum result reduces to the principle of least action.
0, the quantum result reduces to the principle of least action.
It is appropriate to remark that the demarcation between the domains of quantum and classical theory does not necessarily coincide with the one separating macroscopic objects from microscopic ones. (See the next example dealing with a wristwatch and a microprocessor.) The previous criterion for the transition can be generalized to the quantum criterion:14 If an action (or a parameter characterizing the physical situation or phenomenon that has the dimension of action) has a numerical value comparable to Planck's constant, then the behavior of the system must be described using quantum physics. If the action is much larger than ![[h-bar]](newton_mechanics_files/planck.gif) , classical theory offers an approximation sufficiently accurate for most purposes. So the magnitude of the action characterizes the limits of validity of classical theories.
, classical theory offers an approximation sufficiently accurate for most purposes. So the magnitude of the action characterizes the limits of validity of classical theories.
Here we give two examples for which the typical magnitude of the action can be successfully estimated from a procedure based on dimensional analysis. A mechanical wristwatch15 has moving parts with an approximate size d![[approximate]](newton_mechanics_files/ap.gif) 10–4 m, mass m
10–4 m, mass m![[approximate]](newton_mechanics_files/ap.gif) 10–4 kg, and typical time t
10–4 kg, and typical time t![[approximate]](newton_mechanics_files/ap.gif) 1 s. So the characteristic action using dimensional analysis (the unit of S is J s) is S
1 s. So the characteristic action using dimensional analysis (the unit of S is J s) is S![[approximate]](newton_mechanics_files/ap.gif) md2 t–1
md2 t–1![[approximate]](newton_mechanics_files/ap.gif) 10–12 J s
10–12 J s![[approximate]](newton_mechanics_files/ap.gif) 1022
1022![[h-bar]](newton_mechanics_files/planck.gif) .
.
The microprocessor is the heart of every computer. The first Pentium processor (2×2 cm) was made using 0.8 µm technology, which means that the thinnest wires were of size 0.8 µm (d![[approximate]](newton_mechanics_files/ap.gif) 10–6 m). Because it is an electronic device, the operation of the microprocessor depends on electrons (m
10–6 m). Because it is an electronic device, the operation of the microprocessor depends on electrons (m![[approximate]](newton_mechanics_files/ap.gif) 10–30 kg). The processor executes instructions during clock cycles. So the power of processor is approximately given by the maximum clock speed, which was 60 MHz for the first Pentium chip, corresponding to the angular frequency
10–30 kg). The processor executes instructions during clock cycles. So the power of processor is approximately given by the maximum clock speed, which was 60 MHz for the first Pentium chip, corresponding to the angular frequency 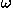
![[approximate]](newton_mechanics_files/ap.gif) 400 MHz. The typical action is represented by S
400 MHz. The typical action is represented by S![[approximate]](newton_mechanics_files/ap.gif) md2
md2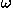
![[approximate]](newton_mechanics_files/ap.gif) 4×10–34 J s
4×10–34 J s![[approximate]](newton_mechanics_files/ap.gif) 4
4![[h-bar]](newton_mechanics_files/planck.gif) . Although these two systems are comparable in size, the result is that the maker of a mechanical watch needs to know nothing about quantum theory, whereas the creators of microprocessors, the basic constituents of modern information technology, must use quantum theory to design their chips.
. Although these two systems are comparable in size, the result is that the maker of a mechanical watch needs to know nothing about quantum theory, whereas the creators of microprocessors, the basic constituents of modern information technology, must use quantum theory to design their chips.
V. CONCLUSION
We have obtained Newton's second law from the principle of least action only for conservative forces, for which there exists a potential function. But the Newtonian formulation of classical mechanics extends readily from this conservative case to nonconservative (dissipative) cases like friction. Are Newton's laws of motion more general than the principle of least action? The answer is again in Feynman's lectures.16 At the microscopic level, there are no dissipative forces. Friction appears only because we neglect microscopic complications resulting from a large number of interacting particles, for which it would be practically impossible to carry out an exact analysis. Although the Newtonian formulation helps effectively to eliminate complications such as the case of friction, Newton's laws cannot be extrapolated to things that are very small or very fast or very large. Indeed, it turns out that the fundamental laws can be set in the form of a principle of least action. From a principle of least action we can derive Maxwell's equations,17 and can use this principle in relativity10 if we find the correct form for the action. The action is very important in many fields of modern physics. We believe that students should be introduced to it early and that the present approach18 is one possible way of doing so.
ACKNOWLEDGMENTS
This paper was written after reading Taylor and Wheeler's book10 and Taylor's materials8 on quantum mechanics. We would like to thank Edwin F. Taylor for providing the book, materials, and helpful comments on this paper. We are also grateful to Slavko Chalupka of the P. J. Safarik University, who discussed with us many of the problems mentioned in the paper and also encouraged us.
REFERENCES
Citation links [e.g., Phys. Rev. D 40, 2172 (1989)] go to online journal abstracts. Other links (see Reference Information) are available with your current login. Navigation of links may be more efficient using a second browser window.
-
R. P. Feynman, R. B. Leighton, and M. Sands, The Feynman Lectures on Physics (Addison-Wesley, Reading, MA, 1964), Vol. 2, Chap. 19.
first citation in article
-
L. D. Landau and E. M. Lifshitz, Mechanics (Butterworth-Heinemann, Oxford, 1976), Sec. 1.2.
first citation in article
-
W. R. Hamilton, "On a general method of expressing the paths of light,
and of the planets by the coefficients of a characteristic function,"
Dublin University Review and Quarterly Magazine 1, 795–826 (1833), available at
 http://www.maths.tcd.ie/pub/HistMath/People/Hamilton/Papers.html
http://www.maths.tcd.ie/pub/HistMath/People/Hamilton/Papers.html , edited by David R. Wilkins.
first citation in article
, edited by David R. Wilkins.
first citation in article
-
Reference 1, p. 19-8.
first citation in article
-
Our analysis will consider Hamilton's principle in the form that
describes the mechanics of conservative systems (or generalized
potentials). On the other hand, there exists an extension of Hamilton's
principle that includes nonconservative and nonholomonic systems. See
H. Goldstein, Classical Mechanics (Addison-Wesley, New York, 1970), Chaps. 2–4.
first citation in article
-
The contents of this article were taught by the first author as a
special topic in a semester quantum mechanics course developed after
Taylor's course (Ref. 8) for future teachers of physics at the Faculty
of Science, P. J. Safarik University, Kosice, Slovakia. It was also
tried for three months in a special physics seminar devoted to modern
physics at a secondary school, Gymnazium of J. A. Rayman, Presov, in
Slovakia. first citation in article
-
Reference 1, p. 19-3.
first citation in article
-
The basic idea of using computers comes from E. F. Taylor;
see especially p. 192 in E. F. Taylor, S. Vokos, J. M. O'Meara, and N.
S. Thornber, "Teaching Feynman's sum over paths quantum theory," Comput. Phys. 12, 190–199 (1998);
and E. F. Taylor, Demystifying Quantum Mechanics, a workbook for quantum mechanics available at  http://www.eftaylor.com
http://www.eftaylor.com . Our software is based on Taylor's software which accompanies his workbook.
first citation in article
. Our software is based on Taylor's software which accompanies his workbook.
first citation in article
-
This minimum condition can be obtained without calculus if we use the expression x = b/2a for the position of the vertex of a parabola described by y = ax2 + bx + c.
first citation in article
-
A very similar, easy, and successful variational method has been
applied in general relativity in E. F. Taylor and J. A. Wheeler, Exploring Black Holes: An Introduction to General Relativity (Addison-Wesley Longman, New York, 2000).
first citation in article
-
This term can be derived from a Taylor's series. See E. W. Schmid, G. Spit, and W. Losch, Theoretical Physics on the Personal Computer (Springer-Verlag, Berlin, 1988), Chap. 2, p. 14.
first citation in article
-
See the following advanced texts: R. P. Feynman and A. R. Hibbs, Quantum Mechanics and Path Integrals (McGraw-Hill, New York, 1965);
or L. S. Schulman, Techniques and Applications of Path Integration (Wiley, New York, 1996).
first citation in article
-
Reference 1, p. 19-9.
first citation in article
-
E. H. Wichman, Quantum Physics (McGraw Hill, New York, 1967), Sec. 1.20
or J. M. Lévy-Leblond and F. Balibar, QUANTICS: Rudiments of Quantum Physics (North-Holland, New York, 1990), Sec. 1.3.
first citation in article
-
The example dealing with a wristwatch was taken from Ref. 14. According
to Ref. 14 (both books), dimensional analysis with a general quantum
criterion allows us to determine the quantum (or classical) nature of
many phenomena (for example, a thrown stone, swinging pendulum, radio
antenna, oscillating electrical circuit, hydrogen atom, salt crystal,
superfluid helium, nucleus, diffracted photon, Coulomb and nuclear
scattering of
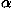 particles).
first citation in article
particles).
first citation in article
-
Reference 1, p. 19-7.
first citation in article
-
L. D. Landau and E. M. Lifshitz, The Classical Theory of Fields (Pergamon, New York, 1975), Chap. 4, pp. 66–75.
first citation in article
-
To obtain draft exercises, software and more detailed information, see
 http://www.LeastAction.host.sk
http://www.LeastAction.host.sk or the mirror site
or the mirror site  http://LeastAction.topcities.com
http://LeastAction.topcities.com .
first citation in article
.
first citation in article
CITING ARTICLES
This list contains links to other online articles that cite the article currently being viewed.
-
Hamilton's principle: Why is the integrated difference of the kinetic and potential energy minimized?
Alberto G. Rojo, Am. J. Phys. 73, 831 (2005)
-
Getting the most action out of least action: A proposal
Thomas A. Moore, Am. J. Phys. 72, 522 (2004)
-
From conservation of energy to the principle of least action: A story line
Jozef Hanc et al., Am. J. Phys. 72, 514 (2004)
-
Deriving Lagrange's equations using elementary calculus
Jozef Hanc et al., Am. J. Phys. 72, 510 (2004)
-
Symmetries and conservation laws: Consequences of Noether's theorem
Jozef Hanc et al., Am. J. Phys. 72, 428 (2004)
FIGURES
 Full figure (4 kB)
Full figure (4 kB)Fig. 1. Two nearby worldlines (height vs elapsed time) xA(t) and xB(t), where xA(t) represents the actual particle's worldline and xB(t) is an alternative worldline, which differs from xA(t) only on section A, which is modified as a new section B. First citation in article
 Full figure (18 kB)
Full figure (18 kB)Fig. 2. A worldline of a particle in the Earth's gravitational field. At this point students know only that for every path represented by a worldline x(t), there exists one number, which is called the action S and that the real path obeys the principle of least action. The software shows students how the principle of least action leads to a unique worldline. Students can choose any worldline for the particle by selecting points (events) that the computer connects with a line. Students drag these points while the computer immediately displays the value of the action S and the table of acceleration or other quantities (position, velocity, momentum, energy) describing the motion. Students soon discover that the path with minimal action has the same acceleration (–9.8 m/s2) at each point, which describes free fall due to gravity. The path that satisfies the principle of least action also conserves total energy. First citation in article
 Full figure (4 kB)
Full figure (4 kB)Fig. 3. Some of the possible motions of a free particle. The true path is represented by a straight worldline, as we know from Newton's first law. First citation in article
 Full figure (3 kB)
Full figure (3 kB)Fig. 4. Consider a broken worldline 1234. According to the triangle inequality, the action for the broken worldline 123 is greater than the action for line segment 13. It follows that the broken worldline 134 has a lower action than 1234. For 134 we can use the triangle inequality again, so that the action for segment 14 is less than the one for 134, and thereby less than the action for 1234. First citation in article
 Full figure (5 kB)
Full figure (5 kB)Fig. 5. Section of worldline (represented by two connected straight-line segments) of a particle moving in the potential field described by PE(x). The events 1, 2, and 3 are three successive events on the particle's worldline. All space and time coordinates are fixed, with the exception of x2, which we change to satisfy the principle of least action. First citation in article
FOOTNOTES
aElectronic mail: jozef.hanc@tuke.sk
bElectronic mail: tuleja@stonline.sk
cElectronic mail: hancova@science.upjs.sk
Up: Issue Table of Contents
Go to: Previous Article | Next Article
Other formats: HTML (smaller files) | PDF (248 kB)
![<i>S</i> [equivalent] [integral]<sub><i>t</i><sub>1</sub></sub><sup><i>t</i><sub>2</sub></sup>(KE – PE)d<i>t</i>.](newton_mechanics_files/386_1m0.gif)
 Figure 1.
Figure 1.  Figure 2.
Figure 2.  Figure 3.
Figure 3. 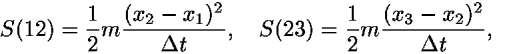
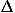 t is the difference between the corresponding times.
t is the difference between the corresponding times. 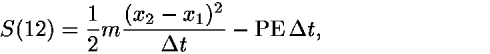
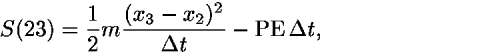
![[infinity]](newton_mechanics_files/infin.gif) , it holds for any continuous smooth worldline. The action has the smallest value for a straight worldline connecting the events, that is, the motion corresponds to constant velocity.
, it holds for any continuous smooth worldline. The action has the smallest value for a straight worldline connecting the events, that is, the motion corresponds to constant velocity.  Figure 4.
Figure 4.  Figure 5.
Figure 5. 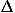 t:
t: 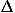 t, this term gives the instantaneous acceleration a at the point 2. Hence, we obtain
t, this term gives the instantaneous acceleration a at the point 2. Hence, we obtain  so that we would cover the entire worldline that describes the motion of the particle. For each of these segments the outcome yields the same Eq. (15). So we have found the connection between the principle of least action and Newton's second law. The worldline representing the path with minimal (stationary) action is the one satisfying Newton's law.
so that we would cover the entire worldline that describes the motion of the particle. For each of these segments the outcome yields the same Eq. (15). So we have found the connection between the principle of least action and Newton's second law. The worldline representing the path with minimal (stationary) action is the one satisfying Newton's law. 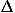 t, the time between the midpoints of the segments, the rate in Eq. (14a) represents the average acceleration.
t, the time between the midpoints of the segments, the rate in Eq. (14a) represents the average acceleration. 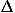 tA and
tA and 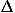 tB for segments A and B,
tB for segments A and B, 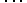 works as follows: The probability that a particle starting at point 1 at the time t1 will arrive at point 2 at time t2 is the square of probability amplitude. The total amplitude can be written as the sum of the amplitudes for each possible path [worldline] for each way of arrival. For every x(t)
works as follows: The probability that a particle starting at point 1 at the time t1 will arrive at point 2 at time t2 is the square of probability amplitude. The total amplitude can be written as the sum of the amplitudes for each possible path [worldline] for each way of arrival. For every x(t)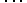 we have to calculate an amplitude. Then we add them all together. The amplitude is proportional to some constant times exp(iS/
we have to calculate an amplitude. Then we add them all together. The amplitude is proportional to some constant times exp(iS/![[h-bar]](newton_mechanics_files/planck.gif) ), where S is action for that path."
), where S is action for that path." ![[h-bar]](newton_mechanics_files/planck.gif) (as is the typical situation for systems described successfully by classical mechanics), we can say roughly that the amplitudes for all paths have very different phases and cancel out in taking the sum, except for those that are extremely close to the path with minimal action. So in the classical limit,
(as is the typical situation for systems described successfully by classical mechanics), we can say roughly that the amplitudes for all paths have very different phases and cancel out in taking the sum, except for those that are extremely close to the path with minimal action. So in the classical limit, ![[h-bar]](newton_mechanics_files/planck.gif)
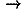 0, the quantum result reduces to the principle of least action.
0, the quantum result reduces to the principle of least action. ![[h-bar]](newton_mechanics_files/planck.gif) , classical theory offers an approximation sufficiently accurate for most purposes. So the magnitude of the action characterizes the limits of validity of classical theories.
, classical theory offers an approximation sufficiently accurate for most purposes. So the magnitude of the action characterizes the limits of validity of classical theories. ![[approximate]](newton_mechanics_files/ap.gif) 10–4 m, mass m
10–4 m, mass m![[approximate]](newton_mechanics_files/ap.gif) 10–4 kg, and typical time t
10–4 kg, and typical time t![[approximate]](newton_mechanics_files/ap.gif) 1 s. So the characteristic action using dimensional analysis (the unit of S is J s) is S
1 s. So the characteristic action using dimensional analysis (the unit of S is J s) is S![[approximate]](newton_mechanics_files/ap.gif) md2 t–1
md2 t–1![[approximate]](newton_mechanics_files/ap.gif) 10–12 J s
10–12 J s![[approximate]](newton_mechanics_files/ap.gif) 1022
1022![[h-bar]](newton_mechanics_files/planck.gif) .
. ![[approximate]](newton_mechanics_files/ap.gif) 10–6 m). Because it is an electronic device, the operation of the microprocessor depends on electrons (m
10–6 m). Because it is an electronic device, the operation of the microprocessor depends on electrons (m![[approximate]](newton_mechanics_files/ap.gif) 10–30 kg). The processor executes instructions during clock cycles. So the power of processor is approximately given by the maximum clock speed, which was 60 MHz for the first Pentium chip, corresponding to the angular frequency
10–30 kg). The processor executes instructions during clock cycles. So the power of processor is approximately given by the maximum clock speed, which was 60 MHz for the first Pentium chip, corresponding to the angular frequency 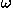
![[approximate]](newton_mechanics_files/ap.gif) 400 MHz. The typical action is represented by S
400 MHz. The typical action is represented by S![[approximate]](newton_mechanics_files/ap.gif) md2
md2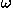
![[approximate]](newton_mechanics_files/ap.gif) 4×10–34 J s
4×10–34 J s![[approximate]](newton_mechanics_files/ap.gif) 4
4![[h-bar]](newton_mechanics_files/planck.gif) . Although these two systems are comparable in size, the result is that the maker of a mechanical watch needs to know nothing about quantum theory, whereas the creators of microprocessors, the basic constituents of modern information technology, must use quantum theory to design their chips.
. Although these two systems are comparable in size, the result is that the maker of a mechanical watch needs to know nothing about quantum theory, whereas the creators of microprocessors, the basic constituents of modern information technology, must use quantum theory to design their chips.  http://www.maths.tcd.ie/pub/HistMath/People/Hamilton/Papers.html
http://www.maths.tcd.ie/pub/HistMath/People/Hamilton/Papers.html , edited by David R. Wilkins.
first citation in article
, edited by David R. Wilkins.
first citation in article  http://www.eftaylor.com
http://www.eftaylor.com . Our software is based on Taylor's software which accompanies his workbook.
first citation in article
. Our software is based on Taylor's software which accompanies his workbook.
first citation in article  particles).
first citation in article
particles).
first citation in article  http://www.LeastAction.host.sk
http://www.LeastAction.host.sk or the mirror site
or the mirror site  http://LeastAction.topcities.com
http://LeastAction.topcities.com .
first citation in article
.
first citation in article  Full figure (4 kB)
Full figure (4 kB) Full figure (18 kB)
Full figure (18 kB) Full figure (4 kB)
Full figure (4 kB) Full figure (3 kB)
Full figure (3 kB) Full figure (5 kB)
Full figure (5 kB)