American Journal of Physics, Vol. 72, No. 4, pp. 522–527, April 2004
©2004 American Association of Physics Teachers. All rights reserved.
Getting the most action out of least action: A proposal
Thomas A. Moorea)
Department of Physics and Astronomy, Pomona College, 610 N. College Avenue, Claremont, California 91711
Received: 8 September 2003; accepted: 12 December 2003Lagrangian methods lie at the foundation of contemporary theoretical physics. Several recent articles have explored the possibility of making the principle of least action and Lagrangian methods a part of the first-year physics curriculum. I examine some of this proposal's implications for subsequent courses in the undergraduate physics major, and focus on the influence that this proposal might have on the selection of topics and the opportunities this proposal presents for teaching these courses in a more contemporary way. Many of these ideas are relevant even if students first learn Lagrangian methods in a sophomore mechanics course. © 2004 American Association of Physics Teachers.
Contents
I. INTRODUCTION
Hamilton's principle,1 more generally known as the principle of least action (particularly since the publication of Feynman's lectures2) has played a seminal role in the development of theoretical physics in the latter part of the 20th century. Lagrangian methods that extend this principle lie at the heart of general relativity, quantum field theory, and the standard model of particle physics, and such methods play a crucial role in conceptually framing and expressing these theories.
Edwin Taylor has recently argued that this principle provides a simple but powerful framework for unifying Newtonian mechanics, relativity, and quantum mechanics,3 and he and his collaborators have begun to lay the foundations for teaching the principle in the introductory course.4,5,6,7,8 If we presume that this proposal is possible and desirable, it has implications for subsequent courses in the physics major. In this article, I will examine some of these implications, focusing on new opportunities that teaching least action in the introductory course makes possible, as well as on what changes in upper-level courses might best support these opportunities in subsequent courses.
My purpose is not to describe a new upper-level curriculum in detail. Instead, I hope that by presenting an overview of the issues and providing references to some available resources, I will provide some guidance to those who might develop such curricula. This article also might be interesting to those seeking to modernize the upper-level courses that follow an intermediate mechanics course which discusses Lagrangian methods.
II. THE MODERN PHYSICS COURSE
Most upper-level physics curricula open with a course in "modern physics," which for the sake of argument in what follows, I will assume to be a sophomore-level class that at least discusses special relativity, some basic quantum theory, atomic and nuclear physics, and perhaps some particle physics. In a curriculum where the classical principle of least action is taught in introductory physics, the modern physics course might be reworked somewhat to address two important goals: connect the classical principle of least action with quantum mechanics and relativity, and build a solid foundation for using the principle in subsequent courses. I will discuss the link to quantum mechanics first (for reasons that will become clearer as we go).
Taylor, Vokos, O'Meara, and Thornber have recently published a curricular plan that connects quantum mechanics with the principle of least action at a level that seems appropriate for sophomores.9 This plan starts with the students working through the first half of Feynman's popular book QED.10 Feynman's book demonstrates that it is possible to explain the results of classical optics in a variety of practical situations using the following simple model: a photon explores all possible paths between emission and detection, we imagine the photon traveling along each possible path to carry an arrow that rotates a number of times that is proportional to the action along that path, and the probability that the photon will be observed at the detection event is proportional to the squared length of the vector sum of the final arrows for all the paths that the photon explores. Sophomore-level majors (unlike Feynman's intended audience) should be able to understand that the arrows are visual representations of complex numbers, but this visualization is powerful and useful even when students can do the calculations with complex numbers.
The fundamental problem with the "explore all paths" model is that actually summing the arrows over all possible paths is a daunting task. Taylor and his collaborators make this task simpler by providing computer programs that compute the sums for various simple paths so that students can explore the implications of the model. Building on this foundation, Taylor and his collaborators (aided by more programs) then extend Feynman's description to help students discover methods for handling free electrons and then electrons with potential energy, the concept of a wave function, the concept of the free-particle propagator, and ultimately the concept of a bound-state wave function, all with very little mathematics.
The method Taylor and his collaborators use to develop the free-particle propagator illustrates their general approach to making difficult ideas more accessible. The key to making the "explore many paths" approach practical is to get rid of the summation over all possible paths. The world line through spacetime between a given starting event a and a given ending event b that has the least action is by definition the world line along which the particle's arrow undergoes the fewest turns from start to finish. With the help of the computer programs, a student can find that the only paths that contribute significantly to the arrow representing the final sum at event b are those contributing final arrows that make an angle of less than 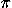 with the arrow contributed by the world line of least action; neither the length nor the direction of the sum is much affected if one ignores all other paths. Indeed, one finds that for a free particle, the direction (in the complex plane) of the arrow representing the sum at b is always rotated by 45° relative to the direction of the arrow contributed by the least-action world line at b (which in turn is simply a rotated version of the arrow at the initial event a), and the sum's magnitude depends on how far a path must deviate from the least-action world line to yield a contributed arrow that makes an angle of
with the arrow contributed by the world line of least action; neither the length nor the direction of the sum is much affected if one ignores all other paths. Indeed, one finds that for a free particle, the direction (in the complex plane) of the arrow representing the sum at b is always rotated by 45° relative to the direction of the arrow contributed by the least-action world line at b (which in turn is simply a rotated version of the arrow at the initial event a), and the sum's magnitude depends on how far a path must deviate from the least-action world line to yield a contributed arrow that makes an angle of 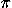 with the least-action arrow.
with the least-action arrow.
Therefore it should be possible in principle to forego the sum entirely and calculate the arrow representing the sum over all paths by rotating the direction of the arrow contributed by the single least-action path by 45° and multiplying by a factor that specifies the degree to which small deviations from this path affect the angle of the path's contributed arrow. For a free particle, this factor can only be a function of the particle's mass m, Planck's constant h, the time interval between the initial and final events, and the spatial separation of those events. Taylor and his collaborators9 argue that we can determine the correct expression for this factor by assuming that a free-particle wave function which is uniform over space at a certain time must remain uniform as time passes (a result required by symmetry). We can consider any wave function at a given time to be a set of arrows (that is, complex numbers) distributed over space. Assume that we know the wave function arrows 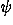 (xi,t0) at various positions xi at some initial time t0. The arrow
(xi,t0) at various positions xi at some initial time t0. The arrow 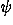 (x,t) at a different position x and later time t is determined by determining the sum of the arrows contributed by all paths starting from the arrow
(x,t) at a different position x and later time t is determined by determining the sum of the arrows contributed by all paths starting from the arrow 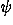 (xi,t0) at a given xi at time t0 and arriving at position x and time t, and then summing over all xi (see Fig. 1). For the free particle, we can do the sum over all paths by calculating the arrow contributed by the least-action path from xi,t0 to x, t (which is a straight world line for a free particle) and use a formula (rule) involving h, m, t–t0, and x–xi to convert this arrow to an arrow representing the sum over all paths. By using a program constructed for this purpose, students can experiment with different rules until they find one that preserves the uniform wave function. The process is quite intuitive and requires very little mathematics.
(xi,t0) at a given xi at time t0 and arriving at position x and time t, and then summing over all xi (see Fig. 1). For the free particle, we can do the sum over all paths by calculating the arrow contributed by the least-action path from xi,t0 to x, t (which is a straight world line for a free particle) and use a formula (rule) involving h, m, t–t0, and x–xi to convert this arrow to an arrow representing the sum over all paths. By using a program constructed for this purpose, students can experiment with different rules until they find one that preserves the uniform wave function. The process is quite intuitive and requires very little mathematics.
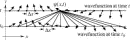 Figure 1.
Figure 1. Once we know how to generate a future wave function from a past one, we can generalize to particles that are not free and begin to explore both stationary and dynamic states of bound particles.9 After developing the general concept of a stationary state, we might introduce the Schrödinger equation and explore bound states of other systems in a more conventional manner.
The approach in Ref. 9 is plausibly accessible to sophomore-level physics majors, and has the advantage of giving these students a deeper, more intuitive, and perhaps more engaging understanding of quantum mechanics than one typically gets in a modern physics course. Moreover, this approach is the only way that I know in which we might plausibly link the classical principle of least action and quantum mechanics at this level. This approach, however, will take a fair amount of class time, and thus will probably displace some other topics usually covered in such a course.11
Next I would like to discuss the treatment of special relativity in the modern physics course. The argument about the propagator assumes that the reader understands what events, world lines, and spacetime diagrams are (Fig. 1 is essentially a spacetime diagram). Therefore, a careful treatment of these concepts in the relativity portion of the course is essential for the success of the quantum section. My experience is that taking the time to teach students to use spacetime diagrams and the geometric analogy to relativity before teaching the Lorentz transformation equations greatly improves their understanding. Students understand much better the meaning of the Lorentz transformation equations after they have seen a spacetime diagram that shows the axes for two different reference frames, and after they have understood the crucial differences between coordinate measurements and the invariant spacetime interval.
The other topic that needs to be explored is the concept of a four-vector. This concept not only makes the relationship between energy, momentum, and mass much easier to understand, but it provides an essential foundation for any future application of Lagrangian methods to special relativity, general relativity, or electricity and magnetism. This course is not where we should introduce index notation and the Einstein summation convention, but most students at this level understand column vectors and matrix multiplication, and we can go a long way with these tools and explore the most crucial characteristics of four-vectors (such as their transformation properties, the invariance of a four-vector's magnitude, the invariance of the dot product of four-vectors, and the frame-independence of four-vector equations).
This part of the course also should link the classical principle of least action with the principle that a straight world line is the world line of longest proper time between two given events (the latter is easily proved using an elementary argument12,13 and should be a part of the development of the concept of proper time). The action S for a relativistic free particle for a given world line can be written as
![<i>S</i> = –<i>m</i><i>c</i><sup>2</sup>[integral]<i>d</i> <i>tau</i>,](moore_action_files/522_1m0.gif)
where c is the speed of light, and the integral yields the total proper time measured along the path. The minus sign ensures that the action is a minimum for whatever path has maximal proper time, and the factor mc2 gives the action the appropriate units and the correct linear dependence on the particle's mass.
We can write Eq. (1) in the form of a coordinate-time integration over a Lagrangian as follows:
![<i>S</i> = –<i>m</i><i>c</i><sup>2</sup>[integral] ((<i>d</i> <i>tau</i>)/<i>d</i><i>t</i>) <i>d</i><i>t</i> = –<i>m</i><i>c</i><sup>2</sup>[integral] sqrt(1–((<i>nu</i><sup>2</sup>)/<i>c</i><sup>2</sup>)) <i>d</i><i>t</i>,](moore_action_files/522_1m1.gif)
which implies that

A simple application of the Euler–Lagrange equations and some basic calculus establishes that the particle's velocity components must be constant. We see, therefore, that we can develop a relativistic principle of least-action for a free particle and obtain the constant-velocity result that we know must be true from other arguments. This result supports the idea (used in the quantum section) that the world line of least action for even a relativistic free particle is indeed a straight world line, and Eq. (2b) is an essential first step in developing an electromagnetic Lagrangian.
Such a discussion would imply a relativity section that is three to four weeks long, which is more time than is usually spent on the topic. In what follows, however, I will show that this discussion would open up significant opportunities for subsequent courses. Because applications of relativity are increasingly important in modern technology, a solid understanding of relativity is more important to physicists and engineers now than it was even two decades ago.14
III. THE INTERMEDIATE MECHANICS COURSE
The next course a typical physics major might encounter would be one in intermediate classical mechanics, which typically discusses subjects such as orbital motion, damped and driven harmonic oscillators, rotation of rigid bodies, and perhaps even some chaos and non-linear dynamics. Texts for this course commonly include a discussion of the principle of least action and Lagrangian methods.15 If these ideas are thoroughly discussed in the introductory course, then some time would become available in this course. My recommendation is that at least some of this extra time be spent exploring the application of Lagrangian methods to continuous media. This application is important because the same methods apply to fields, so this discussion of continuous media would provide essential background for any subsequent application of Lagrangian methods to the electromagnetic field. Reference 16 presents a very nice discussion of continuous media.
IV. QUANTUM MECHANICS
Most undergraduate major programs include a quantum mechanics course in the junior or senior year. I will assume that students in this course are familiar with partial derivatives, complex numbers, looking up integrals, and Taylor-series expansions.
A crucial first step in this course would be to firmly and formally connect the explore all paths model presented in the sophomore course with the time-dependent Schrödinger equation. Once this connection has been made, the rest of the course can be taught in the standard way. In what follows, I will briefly sketch the logic of the argument: more details can be found in Ref. 17.
In the sophomore-level course, students should have discovered that for a free particle, the propagator function that species the contribution to the quantum amplitude (arrow) 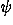 (x,t) made by arrows of the particle's wave function within a sufficiently small range
(x,t) made by arrows of the particle's wave function within a sufficiently small range 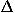 xi around the position xi at an earlier time t0 is given by
xi around the position xi at an earlier time t0 is given by
![<i>K</i>(<i>x</i>,<i>t</i>,<i>x</i><sub><i>i</i></sub>,<i>t</i><sub>0</sub>)<i>psi</i>(<i>x</i><sub><i>i</i></sub>,<i>t</i><sub>0</sub>)<i>Delta</i> <i>x</i><sub><i>i</i></sub> = sqrt((<i>m</i>/(<i>h</i>(<i>t</i> – <i>t</i><sub>0</sub>)<i>i</i>))) <i>e</i><sup><i>i</i><i>S</i><sub>direct</sub>/[h-bar]</sup><i>psi</i>(<i>x</i><sub><i>i</i></sub>,<i>t</i><sub>0</sub>)<i>Delta</i> <i>x</i><sub><i>i</i></sub>,](moore_action_files/522_1m3.gif)
where Sdirect is the action measured along the straight worldline from xi,t0 to x, t. For a free particle moving in one dimension with a constant potential energy V, the value of Sdirect is simply
![<i>S</i><sub>direct</sub> = (<i>T</i> – <i>V</i>)<i>Delta</i> <i>t</i> = [(1/2) <i>m</i>(((<i>x</i> – <i>x</i><sub><i>i</i></sub>)/(<i>Delta</i> <i>t</i>)))<sup>2</sup> – <i>V</i>]<i>Delta</i> <i>t</i> = ((<i>m</i><i>u</i><sup>2</sup>)/(2 <i>Delta</i> <i>t</i>)) – <i>V</i> <i>Delta</i> <i>t</i>,](moore_action_files/522_1m4.gif)
where 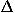 t
t![[equivalent]](moore_action_files/equiv.gif) t–t0 is the (coordinate) time difference between the events and u
t–t0 is the (coordinate) time difference between the events and u![[equivalent]](moore_action_files/equiv.gif) xi–x. So in this case, we have
xi–x. So in this case, we have
![<i>K</i>(<i>x</i>,<i>t</i>,<i>x</i><sub><i>i</i></sub>,<i>t</i><sub>0</sub>) = sqrt((<i>m</i>/(<i>h</i>(<i>t</i> – <i>t</i><sub>0</sub>)<i>i</i>))) exp(((<i>i</i><i>m</i><i>u</i><sup>2</sup>)/(2[h-bar] <i>Delta</i> <i>t</i>)))exp(–((<i>i</i> <i>Delta</i> <i>t</i>)/([h-bar])) <i>V</i>).](moore_action_files/522_1m5.gif)
To find the complete wave function amplitude 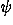 (x,t), we must sum K
(x,t), we must sum K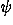 (xi,t0)
(xi,t0)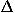 xi over all possible initial positions xi, as schematically shown in Fig. 1. Note that the middle factor in Eq. (5) is the only thing that varies as xi varies, because it will cause u to vary, and this term rotates the phase angle of the resulting complex amplitude. As discussed, arrows rotated by an angle greater than
xi over all possible initial positions xi, as schematically shown in Fig. 1. Note that the middle factor in Eq. (5) is the only thing that varies as xi varies, because it will cause u to vary, and this term rotates the phase angle of the resulting complex amplitude. As discussed, arrows rotated by an angle greater than 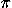 relative to the arrow for u = 0 do not contribute significantly to the result, and we really only need to be concerned about the contributions from the initial positions xi close enough to the final position x so that
relative to the arrow for u = 0 do not contribute significantly to the result, and we really only need to be concerned about the contributions from the initial positions xi close enough to the final position x so that
![((<i>m</i><i>u</i><sup>2</sup>)/(2[h-bar] <i>Delta</i> <i>t</i>)) < <i>pi</i> or <i>u</i><sup>2</sup> < (<i>h</i>/<i>m</i>) <i>Delta</i> <i>t</i>.](moore_action_files/522_1m6.gif)
Equation (6) proves to be the key to using the explore all paths approach to derive the Schrödinger equation. Note that if we choose the time step 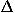 t = t–t0 between the initial and final wave functions to be infinitesimal, then u also must be infinitesimal, which means that the positions of points along all the paths in Fig. 1 that contribute significantly will not be much different from x. Therefore, even if the particle's potential energy varies with position, its value over the range of interest for calculating
t = t–t0 between the initial and final wave functions to be infinitesimal, then u also must be infinitesimal, which means that the positions of points along all the paths in Fig. 1 that contribute significantly will not be much different from x. Therefore, even if the particle's potential energy varies with position, its value over the range of interest for calculating 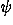 (x,t) will be essentially equal to V(x), its value at x, so Eqs. (3,4,5) apply even to the case of nonuniform V(x) in the limit
(x,t) will be essentially equal to V(x), its value at x, so Eqs. (3,4,5) apply even to the case of nonuniform V(x) in the limit 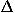 t
t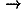 0. The sum over all xi in this limit therefore becomes
0. The sum over all xi in this limit therefore becomes
![<i>psi</i>(<i>x</i>,<i>t</i>) = sqrt((<i>m</i>/(<i>i</i><i>h</i> <i>Delta</i> <i>t</i>))) [integral]<sub>–[infinity]</sub><sup>[infinity]</sup> exp(((<i>i</i><i>m</i><i>u</i><sup>2</sup>)/(2[h-bar] <i>Delta</i> <i>t</i>)))exp(–((<i>i</i> <i>Delta</i> <i>t</i>)/([h-bar])) <i>V</i>(<i>x</i>))<i>psi</i>(<i>x</i> + <i>u</i>,<i>t</i><sub>0</sub>)<i>d</i><i>u</i>,](moore_action_files/522_1m7.gif)
because xi = x + u and dxi = du. If we expand the exponential involving V to order 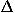 t,
t, 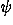 (x + u,t0) to order u2, and do some integrals of the form
(x + u,t0) to order u2, and do some integrals of the form ![[integral]](moore_action_files/int.gif)
![<sub>–[infinity]</sub><sup>[infinity]</sup>](moore_action_files/522_1m8.gif) une–au2du,18 we find that
une–au2du,18 we find that
![<i>psi</i>(<i>x</i>,<i>t</i>) = <i>psi</i>(<i>x</i>,<i>t</i><sub>0</sub>) + 0–(([h-bar] <i>Delta</i> <i>t</i>)/2<i>i</i><i>m</i>) (([partial-derivative]<sup>2</sup><i>psi</i>)/([partial-derivative]<i>x</i><sup>2</sup>))–((<i>i</i> <i>Delta</i> <i>t</i>)/([h-bar])) <i>V</i>(<i>x</i>)<i>psi</i>(<i>x</i>,<i>t</i><sub>0</sub>).](moore_action_files/522_1m9.gif)
If we subtract 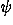 (x,t0) from both sides, multiply through by i
(x,t0) from both sides, multiply through by i![[h-bar]](moore_action_files/planck.gif) /
/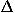 t, and take the limit
t, and take the limit 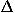 t
t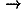 0, we find the time-dependent Schrödinger equation for one dimension. (It is not very difficult to generalize this derivation to three dimensions, but it does not yield any deeper understanding.)
0, we find the time-dependent Schrödinger equation for one dimension. (It is not very difficult to generalize this derivation to three dimensions, but it does not yield any deeper understanding.)
V. ELECTRICITY AND MAGNETISM
The undergraduate curriculum also typically includes a course in electricity and magnetism offered at the sophomore, junior, or senior level. I will assume that this course is offered for juniors and/or seniors and that students have taken a modern physics course and intermediate mechanics course of the type already described.
The first task in this course would be to discuss index notation and the Einstein summation convention, the Lorentz transformation properties of scalars, vectors, and covectors, and the four-gradient. My experience is that juniors and seniors can become comfortable with this material within four to five class sessions if the material is taught carefully.19 The relativistic Lorentz force law provides a good physical context for practicing the notation. In appropriate units,20 this law can be written as

where
![<i>F</i><sup><i>µ</i> <i>nu</i></sup> = [(0, – <i>E</i><sub><i>x</i></sub>, – <i>E</i><sub><i>y</i></sub>, – <i>E</i><sub><i>z</i></sub>; <i>E</i><sub><i>x</i></sub>, 0, – <i>B</i><sub><i>z</i></sub>, <i>B</i><sub><i>y</i></sub>; <i>E</i><sub><i>y</i></sub>, <i>B</i><sub><i>z</i></sub>, 0, – <i>B</i><sub><i>x</i></sub>; <i>E</i><sub><i>z</i></sub>, – <i>B</i><sub><i>y</i></sub>, <i>B</i><sub><i>x</i></sub>, 0)],](moore_action_files/522_1m11.gif)
and u is the charged particle's four-velocity with components ut = [1–
is the charged particle's four-velocity with components ut = [1–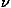 2/c2]–1/2
2/c2]–1/2![[equivalent]](moore_action_files/equiv.gif)
 , ui =
, ui = 
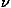 i/c, pµ = mc uµ is the particle's four-momentum, q is its charge,
i/c, pµ = mc uµ is the particle's four-momentum, q is its charge, 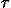 is the proper time measured along its world line and I am using a metric with a timelike signature (+–––). Equation (9) involves scalars, vectors, covectors, and tensors and yet when the sums are written out explicitly, the three spatial components reduce to the Lorentz law taught in introductory physics and the time component reduces to conservation of energy. By examining the transformation properties of all the pieces, students can demonstrate that Eq. (9) must have the same form in all reference frames. It also is a good exercise for students to show that the antisymmetric nature of Fµ
is the proper time measured along its world line and I am using a metric with a timelike signature (+–––). Equation (9) involves scalars, vectors, covectors, and tensors and yet when the sums are written out explicitly, the three spatial components reduce to the Lorentz law taught in introductory physics and the time component reduces to conservation of energy. By examining the transformation properties of all the pieces, students can demonstrate that Eq. (9) must have the same form in all reference frames. It also is a good exercise for students to show that the antisymmetric nature of Fµ ensures that d(pµpµ)/d
ensures that d(pµpµ)/d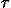 = 0, meaning that the particle's rest mass m = pµpµ is fixed.
= 0, meaning that the particle's rest mass m = pµpµ is fixed.
To fully connect electricity and magnetism with the principle of least action, we also must develop the concept of the magnetic potential A. Textbooks at this level avoid or marginalize the magnetic potential, partly because when it is presented in the usual way, it can be a tricky and abstract concept. However, there are ways to make the magnetic potential more accessible,21 and there are some good reasons to discuss it fully even if we ignore the principle of least action.22
One possible story line for introducing the four-potential is made possible by the principle of least action. The action for a non-relativistic particle moving in a static electric field is
<i>d</i><i>t</i> = [integral]((1/2) <i>m</i> <i>nu</i><sup>2</sup> – <i>q</i> <i>phi</i>)<i>d</i><i>t</i>.](moore_action_files/522_1m12.gif)
Our goal is to see if we can guess the appropriate relativistic action for this case. We already know how to generalize the kinetic energy part; the action for a free particle is given in Eq. (2a). Like this part, whatever we add to the action to account for the field must be a relativistic scalar. But is the electric potential 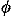 a relativistic scalar or something else? By considering the field between the plates of a parallel-plate capacitor when viewed in a frame moving parallel to the plates, it can be quickly argued that
a relativistic scalar or something else? By considering the field between the plates of a parallel-plate capacitor when viewed in a frame moving parallel to the plates, it can be quickly argued that 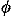 must transform like the time component of a four-vector. So in a fully relativistic expression for the action, the electromagnetic field must appear in the form of a four-vector that we will call Aµ. However, the term we add to the Lagrangian must be a relativistic scalar, so the term must be the dot product of Aµ and some other four-vector. The only available four-vector in the case of a point particle is the particle's own four-velocity uµ. So we propose a relativistic action of the form
must transform like the time component of a four-vector. So in a fully relativistic expression for the action, the electromagnetic field must appear in the form of a four-vector that we will call Aµ. However, the term we add to the Lagrangian must be a relativistic scalar, so the term must be the dot product of Aµ and some other four-vector. The only available four-vector in the case of a point particle is the particle's own four-velocity uµ. So we propose a relativistic action of the form
<i>d</i> <i>tau</i> = –[integral](<i>m</i><i>c</i><sup>2</sup> + <i>q</i><i>u</i><sub><i>µ</i></sub><i>A</i><sup><i>µ</i></sup>) ((<i>d</i> <i>tau</i>)/<i>d</i><i>t</i>) <i>d</i><i>t</i>](moore_action_files/522_1m13.gif)
/<i>c</i><sup>2</sup>)) – <i>q</i> <i>phi</i> +(<i>q</i>/<i>c</i>) <b>v · A</b>)<i>d</i><i>t</i>,](moore_action_files/522_1m14.gif)
where the components of A are the spatial components of Aµ. We can easily show that S in Eq. (11b) reduces to Eq. (10) in the non-relativistic limit (except for an extra rest energy term that does not affect the motion).
What kind of motion does this principle imply? Although we can quickly give the result in index notation, let me demonstrate the argument in a form that might be more accessible to a junior physics major. Consider the x component of the Euler–Lagrange equation. The partial derivatives of the Lagrangian in this case are
![(([partial-derivative]<i>L</i>)/([partial-derivative]<i>x</i>)) = –<i>q</i> (([partial-derivative] <i>phi</i>)/([partial-derivative]<i>x</i>))+(<i>q</i>/<i>c</i>) (<i>nu</i><sup><i>x</i></sup> (([partial-derivative]<i>A</i><sup><i>x</i></sup>)/([partial-derivative]<i>x</i>)) + <i>nu</i><sup><i>y</i></sup> (([partial-derivative]<i>A</i><sup><i>y</i></sup>)/([partial-derivative]<i>x</i>)) + <i>nu</i><sup><i>z</i></sup> (([partial-derivative]<i>A</i><sup><i>z</i></sup>)/([partial-derivative]<i>x</i>))),](moore_action_files/522_1m15.gif)
![(([partial-derivative]<i>L</i>)/([partial-derivative] <i>nu</i><sup><i>x</i></sup>)) = ((<i>m</i> <i>nu</i><sup><i>x</i></sup>)/(sqrt(1 – <i>nu</i><sup>2</sup>/<i>c</i><sup>2</sup>)))+(<i>q</i>/<i>c</i>) <i>A</i><sup><i>x</i></sup> = <i>p</i><sup><i>x</i></sup>+(<i>q</i>/<i>c</i>) <i>A</i><sup><i>x</i></sup>,](moore_action_files/522_1m16.gif)
where px is the relativistic momentum. The Euler–Lagrange equations in this case therefore imply that
![((<i>d</i><i>p</i><sup><i>x</i></sup>)/<i>d</i><i>t</i>)+(<i>q</i>/<i>c</i>) ((([partial-derivative]<i>A</i><sup><i>x</i></sup>)/([partial-derivative]<i>t</i>))+(([partial-derivative]<i>A</i><sup><i>x</i></sup>)/([partial-derivative]<i>x</i>)) <i>nu</i><sup><i>x</i></sup>+(([partial-derivative]<i>A</i><sup><i>x</i></sup>)/([partial-derivative]<i>y</i>)) <i>nu</i><sup><i>y</i></sup>+(([partial-derivative]<i>A</i><sup><i>x</i></sup>)/([partial-derivative]<i>z</i>)) <i>nu</i><sup><i>z</i></sup>) = –<i>q</i> (([partial-derivative] <i>phi</i>)/([partial-derivative]<i>x</i>))+(<i>q</i>/<i>c</i>) (<i>nu</i><sup><i>x</i></sup> (([partial-derivative]<i>A</i><sup><i>x</i></sup>)/([partial-derivative]<i>x</i>)) + <i>nu</i><sup><i>y</i></sup> (([partial-derivative]<i>A</i><sup><i>y</i></sup>)/([partial-derivative]<i>x</i>)) + <i>nu</i><sup><i>z</i></sup> (([partial-derivative]<i>A</i><sup><i>z</i></sup>)/([partial-derivative]<i>x</i>))),](moore_action_files/522_1m17.gif)
which implies that
![((<i>d</i><i>p</i><sup><i>x</i></sup>)/<i>d</i><i>t</i>) = –<i>q</i> (([partial-derivative] <i>phi</i>)/([partial-derivative]<i>x</i>))–(<i>q</i>/<i>c</i>) (([partial-derivative]<i>A</i><sup><i>x</i></sup>)/([partial-derivative]<i>t</i>))+(<i>q</i>/<i>c</i>) <i>nu</i><sup><i>y</i></sup>((([partial-derivative]<i>A</i><sup><i>y</i></sup>)/([partial-derivative]<i>x</i>))–(([partial-derivative]<i>A</i><sup><i>x</i></sup>)/([partial-derivative]<i>y</i>)))–(<i>q</i>/<i>c</i>) <i>nu</i><sup><i>z</i></sup> ((([partial-derivative]<i>A</i><sup><i>x</i></sup>)/([partial-derivative]<i>z</i>))–(([partial-derivative]<i>A</i><sup><i>z</i></sup>)/([partial-derivative]<i>x</i>))).](moore_action_files/522_1m18.gif)
The usual definition of the electric field is the force per unit charge on a test charge at rest, so we have
![<i>E</i><sup><i>x</i></sup> = –(1/<i>c</i>) (([partial-derivative]<i>A</i><sup><i>x</i></sup>)/([partial-derivative]<i>t</i>))–(([partial-derivative] <i>phi</i>)/([partial-derivative]<i>x</i>)).](moore_action_files/522_1m19.gif)
If we identify
![<b>B</b> = [del] × <b>A</b>,](moore_action_files/522_1m20.gif)
we can easily see that Eq. (13b) is equivalent to the x component of the Lorentz force law given by Eq. (9a). We also can see quite generally that
![<i>F</i><sup><i>µ</i> <i>nu</i></sup> = [partial-derivative]<sup><i>µ</i></sup><i>A</i><sup><i>nu</i></sup> – [partial-derivative]<sup><i>nu</i></sup><i>A</i><sup><i>µ</i></sup>,](moore_action_files/522_1m21.gif)
and that Faraday's law and div B = 0 are identities implied by Eq. (15).
Once we have gone this far, we can derive the source-dependent Maxwell equations from a plausible principle of least action.23 Students should know from the treatment of continuous media in the intermediate mechanics course that a least-action principle for the electromagnetic field will involve integrating a Lagrangian density over all space and time. This Lagrangian density must be a relativistic scalar and must involve a term that is quadratic in the field quantities. These requirements imply that the resulting Euler–Lagrange equations will produce linear differential equations in the field, which is required for the field to obey the superposition principle. The only plausible candidates for such terms are AµAµ and Fµ Fµ
Fµ . The first of these leads to absurd results, for example, the resulting field equations in the electrostatic case involve
. The first of these leads to absurd results, for example, the resulting field equations in the electrostatic case involve 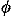 directly, not the derivatives of
directly, not the derivatives of 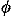 , which does not match Gauss' law. For the second case, we can argue that the sign of the integral has to be negative for the quantity to have a plausible minimum,24 and that we must have a factor of 1/k (where k is Coulomb's constant) to make the units come out right. The Lagrangian density also must involve a term that is linear in the four-current Jµ = [
, which does not match Gauss' law. For the second case, we can argue that the sign of the integral has to be negative for the quantity to have a plausible minimum,24 and that we must have a factor of 1/k (where k is Coulomb's constant) to make the units come out right. The Lagrangian density also must involve a term that is linear in the four-current Jµ = [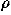 ,j/c], where j is the ordinary current density, so that the sources will appear linearly in the field equation. The only plausible term with the right units in this case is AµJµ. Therefore, the least-action principle for the electromagnetic field must be something like
,j/c], where j is the ordinary current density, so that the sources will appear linearly in the field equation. The only plausible term with the right units in this case is AµJµ. Therefore, the least-action principle for the electromagnetic field must be something like
 <i>F</i><sub><i>µ</i> <i>nu</i></sub><i>F</i><sup><i>µ</i> <i>nu</i></sup> + <i>b</i><i>A</i><sub><i>µ</i></sub><i>J</i><sup><i>µ</i></sup>)<i>d</i><i>t</i> <i>d</i><i>x</i> <i>d</i><i>y</i> <i>d</i><i>z</i> = [integral](–(1/<i>k</i>) [<i>g</i><sup><i>µ</i> <i>alpha</i></sup><i>g</i><sup><i>nu</i> <i>beta</i></sup>([partial-derivative]<sub><i>µ</i></sub><i>A</i><sub><i>nu</i></sub> – [partial-derivative]<sub><i>nu</i></sub><i>A</i><sub><i>µ</i></sub>)([partial-derivative]<sub><i>alpha</i></sub><i>A</i><sub><i>beta</i></sub> – [partial-derivative]<sub><i>beta</i></sub><i>A</i><sub><i>alpha</i></sub>)] + <i>b</i><i>A</i><sub><i>µ</i></sub><i>J</i><sup><i>µ</i></sup>)<i>d</i><i>t</i> <i>d</i><i>x</i> <i>d</i><i>y</i> <i>d</i><i>z</i>,](moore_action_files/522_1m22.gif)
where gµ is the inverse flat-space metric and b is some unitless constant that specifies the relative magnitude and sign of the two terms. The field quantities Aµ play the role of coordinates and the gradients
is the inverse flat-space metric and b is some unitless constant that specifies the relative magnitude and sign of the two terms. The field quantities Aµ play the role of coordinates and the gradients ![[partial-derivative]](moore_action_files/part.gif) µA
µA play the role of "velocities." With only a bit of work,25 the Euler–Lagrange equations yield
play the role of "velocities." With only a bit of work,25 the Euler–Lagrange equations yield
![[partial-derivative]<sub><i>µ</i></sub>([partial-derivative]<sub><i>µ</i></sub><i>A</i><sup><i>nu</i></sup> – [partial-derivative]<sup><i>nu</i></sup><i>A</i><sup><i>µ</i></sup>) = [partial-derivative]<sub><i>µ</i></sub><i>F</i><sup><i>µ</i> <i>nu</i></sup> = –(<i>b</i><i>k</i>/4) <i>J</i><sup><i>nu</i></sup>.](moore_action_files/522_1m23.gif)
If we choose b = –16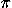 , the time component of Eq. (17) matches Gauss' law. By writing them out, students can discover that the other components spell out the Ampere–Maxwell relation.
, the time component of Eq. (17) matches Gauss' law. By writing them out, students can discover that the other components spell out the Ampere–Maxwell relation.
VI. OTHER INTERESTING APPLICATIONS OF LEAST ACTION
Because many electromagnetic circuits have direct mechanical analogs, we often can use Lagrangian methods to find equations of motion for such circuits, even for very complicated electromechanical circuits. It turns out that we can even handle realistic resistors by treating them as generalized external forces. These issues (along with many other applications of Lagrangian techniques) are beautifully discussed by Wells.26
Another interesting source of applications of the principle of least action to fields at a fairly advanced level is a book written some time ago by Soper.27 This book even includes a discussion of dissipative effects that might be appropriate in an upper-level course.
Once students are used to the principle of least action, other variational calculations become conceptually simpler. Several years ago, Van Baak discussed a variational technique that enables one to solve complicated steady-state circuits without invoking Kirchoff's loop rule.28 Because applying the loop rule requires careful attention to signs, it is a common source of student errors. Van Baak's approach avoids this problem.
Finally, I point out that if students have studied special relativity in some depth and have seen index notation and know about four-vectors, covectors, and tensors, they have a background that provides a great springboard for studying general relativity. The geodesic equations of motion can be treated as a least-action principle. One can even use a Lagrangian to find equations of motion for the gravitational field,29 a method widely used by researchers in the field (particularly those doing numerical simulations).
VII. CONCLUSIONS
My goal has been to reflect on what kinds of changes to the upper-level curriculum might help students take full advantage of an introductory-level exploration of the principle of least action. I have only provided a broad sketch; there is much work to be done before these suggestions can become anything approaching a practical curriculum. The proposed changes would in some cases mean shifting priorities to allow sufficient time for the development of some of the techniques, and I have no doubt that some of the changes would present problems that would have to be worked out.
However, the proposed changes could create a very exciting upper-level curriculum that could more clearly display the deep underlying connections between mechanics, relativity, electrodynamics, and quantum mechanics. These changes would give us a thoroughly 21st-century physics curriculum that teaches viewpoints and techniques currently used by researchers. The principle of least action is among the most beautiful and powerful physical principles ever envisioned. With some vision and effort, the least action principle could become a greater part of the common background of physics undergraduates.
ACKNOWLEDGMENTS
I would like to thank E. F. Taylor, the editors of this special issue, and the reviewers for making valuable suggestions about how to improve this article.
REFERENCES
Citation links [e.g., Phys. Rev. D 40, 2172 (1989)] go to online journal abstracts. Other links (see Reference Information) are available with your current login. Navigation of links may be more efficient using a second browser window.
-
Herbert Goldstein, Charles P. Poole, Jr., and John L. Safko, Classical Mechanics (Addison–Wesley, San Francisco, 2002), 3rd ed., Vol. 1, Chap. 2, pp. 34ff.
first citation in article
-
Richard P. Feynman, Robert B. Leighton, and Matthew Sands, The Feynman Lectures on Physics (Addison–Wesley, Reading, MA, 1964), Vol. 2, Chap. 19, pp. 19–1ff.
first citation in article
-
Edwin F. Taylor, "A call to action," Am. J. Phys. 71, 423–425 (2003). [ISI]
first citation in article
-
Jozef Hanc, Slavomir Tuleja, and Martina Hancova, "Simple derivation of
Newtonian mechanics from the principle of least action," Am. J. Phys. 71, 386–391 (2003). [ISI]
first citation in article
-
Jozef Hanc, Edwin F. Taylor, and Slavomir Tuleja, "Deriving Lagrange's
equations using elementary calculus," Am. J. Phys. (submitted). See
 www.eftaylor.com/leastaction.html
www.eftaylor.com/leastaction.html .
first citation in article
.
first citation in article
-
Edwin F. Taylor and Jozef Hanc, "From conservation of energy to the
principle of least action: A story line," Am. J. Phys. (submitted). See
 www.eftaylor.com/leastaction.html
www.eftaylor.com/leastaction.html .
first citation in article
.
first citation in article
-
Jozef Hanc, Slavomir Tuleja, and Martina Hancova, "Symmetries and
conservation laws: Consequences of Noether's theorem," Am. J. Phys.
(submitted). See
 www.eftaylor.com/leastaction.html
www.eftaylor.com/leastaction.html .
first citation in article
.
first citation in article
-
Jozef Hanc, "The original Euler's calculus-of-variations method: Key to
Lagrangian mechanics for beginners," Am. J. Phys. (submitted). See
 www.eftaylor.com/leastaction.html
www.eftaylor.com/leastaction.html .
first citation in article
.
first citation in article
-
Edwin F. Taylor, Stamatis Vokos, John M. O'Meara, and Nora S. Thornber,
"Teaching Feynman's sum-over-paths quantum theory," Comput. Phys. 12, 190–199 (1998). Current versions of the draft teaching materials and computer programs discussed in this article are available online at
 www.eftaylor.com/download.html#quantum
www.eftaylor.com/download.html#quantum .
first citation in article
.
first citation in article
-
Richard S. Feynman, QED: The Strange Theory of Light and Matter (Princeton U.P., Princeton, 1985).
first citation in article
-
Such modern physics courses often include a discussion of the
historical development of quantum mechanics that would be less relevant
to this approach. Cutting much of this material will help make some
room. first citation in article
-
Edwin F. Taylor and John Archibald Wheeler, Spacetime Physics (Freeman, New York, 1992), 2nd ed., p. 149ff.
first citation in article
-
Thomas A. Moore, A Traveler's Guide to Spacetime (McGraw–Hill, New York, 1995), pp. 86–87. The same argument also appears on pp. 83–84 of Moore's introductory textbook, Six Ideas That Shaped Physics, Unit R: The Laws of Physics are Frame-Independent (McGraw–Hill, New York, 2003), 2nd ed.
first citation in article
-
The relativity of simultaneity has become a very practical engineering
problem for the designers of the global positioning system. Students
can see the delay imposed by light travel time when satellite
communications are used on television. Experimental general relativity
has mushroomed in recent years, and gravitational waves will likely be
discovered in the coming decade. Moreover, aspects of relativistic
cosmology previously considered esoteric are likely to have a large
impact on physics in the next couple of decades. first citation in article
-
Examples include Jerry B. Marion and Stephen T. Thornton, Classical Dynamics of Particles and Systems (Saunders, Fort Worth, 1995), 4th ed.;
Ralph Baierlein, Newtonian Dynamics (McGraw–Hill, New York, 1983); and
Grant R. Fowles, Analytical Mechanics (Saunders, Philadelphia, 1986), 4th ed.
first citation in article
-
Herbert Goldstein, Charles P. Poole, Jr., and John L. Safko, Classical Mechanics
(Addison–Wesley, San Francisco, 2002), 3rd ed. Secs. 13.1 and 13.2 (up
to the middle of p. 563) are at a level suitable for sophomores or
juniors. One would probably not need to derive the Euler–Lagrange
equations the way that they do, but rather state the equations
(appealing to analogy) and show that they work for a simple case (as
the authors do at the top of p. 563). first citation in article
-
Ramamurti Shankar, Principles of Quantum Mechanics (Plenum, New York, 1980), Sec. 8.5, pp. 240–241.
first citation in article
-
The results for these definite integrals given in standard integral tables assume (usually implicitly) that a is real. However, the same results apply even if a is complex, as long as the real part of a>0. See, for example, Milton Abramowitz and Irene A. Stegun, Handbook of Mathematical Functions
(Dover, New York, 1964), p. 302, where no such assumption is made. I am
not sure that it is necessary to have students worry about this issue
unless they ask. first citation in article
-
I regularly teach a junior-level course in general relativity where
students are required to master this material. I have found that there
are some tricks for teaching index notation at this level that are
beyond the scope of this article to discuss in detail, but it helps
greatly if students are explicitly taught to recognize the difference
between free and summed indices, and if they write out expanded
versions of the equations when necessary. Students also should be
required to calculate the time derivative of a product involving an
implied sum and do other exercises where the correct answer depends on
correctly recognizing the implied sums. J. B. Hartle's Gravity
(Addison–Wesley, San Francisco, 2003) is better than most general
relativity books in teaching the notation (and in presenting the entire
subject of relativity to undergraduates). first citation in article
-
We can conveniently combine the advantages of Gaussian and SI units by defining B
![[equivalent]](moore_action_files/equiv.gif) cBconv, where Bconv is the conventional magnetic field measured in teslas. The redefined B
has units of N/C, just like the electric field (with 300 MN/C
corresponding to 1 T.) All electromagnetic equations then take the same
mathematical form as they would in Gaussian units, except that factors
of 4
cBconv, where Bconv is the conventional magnetic field measured in teslas. The redefined B
has units of N/C, just like the electric field (with 300 MN/C
corresponding to 1 T.) All electromagnetic equations then take the same
mathematical form as they would in Gaussian units, except that factors
of 4 become 4
become 4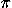 k, where k
is the Coulomb constant. However, the units for all quantities other
than the magnetic field are in SI. This system makes the symmetries
between the electric and magnetic fields apparent (and the equations
much more beautiful) without having to deal with Gaussian units. This
unit system also has the advantage of making it easy to show the
connections between electromagnetic field theory and gravitational
field theory (where the gravitational constant G is not typically suppressed as is the corresponding Coulomb constant k in Gaussian units).
first citation in article
k, where k
is the Coulomb constant. However, the units for all quantities other
than the magnetic field are in SI. This system makes the symmetries
between the electric and magnetic fields apparent (and the equations
much more beautiful) without having to deal with Gaussian units. This
unit system also has the advantage of making it easy to show the
connections between electromagnetic field theory and gravitational
field theory (where the gravitational constant G is not typically suppressed as is the corresponding Coulomb constant k in Gaussian units).
first citation in article
-
For example, A can be given a more physical meaning than often is supposed. In a static situation where
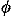 = 0 and a particle moves perpendicular to A, the Euler–Lagrange equations implied by Eq. (11) imply that the quantity p + (q/c)A is constant in time. Just as the scalar potential
= 0 and a particle moves perpendicular to A, the Euler–Lagrange equations implied by Eq. (11) imply that the quantity p + (q/c)A is constant in time. Just as the scalar potential 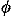 at a point in space near a static charge distribution is the total work
per unit charge that one would have to do on a charged test particle to
move it from infinity to that point, the quantity A/c at
a point in space near a static (and neutral) current distribution is
the total momentum per unit charge that one would have to supply to a
charged test particle to keep it moving from infinity to that position
along a path that is always perpendicular to A. Therefore, if
at a point in space near a static charge distribution is the total work
per unit charge that one would have to do on a charged test particle to
move it from infinity to that point, the quantity A/c at
a point in space near a static (and neutral) current distribution is
the total momentum per unit charge that one would have to supply to a
charged test particle to keep it moving from infinity to that position
along a path that is always perpendicular to A. Therefore, if 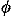 represents potential energy per unit charge, A represents "potential momentum" per unit charge.
first citation in article
represents potential energy per unit charge, A represents "potential momentum" per unit charge.
first citation in article
-
For example, the Aharonov–Bohm effect suggests that the magnetic potential is more fundamental than E and B, and is certainly more directly connected to quantum mechanics. See J. J. Sakurai, Modern Quantum Mechanics, edited by San Fu Tuan (Addison–Wesley, Redwood City, CA, 1985), pp. 136–139, or John S. Townsend, A Modern Approach to Quantum Mechanics
(McGraw–Hill, New York, 1992), pp. 399–404 for good discussions of this
effect. The four-potential also provides significant advantages for
calculating electromagnetic fields: indeed, R. L. Coren of Drexel
University once told me that computer programs used by electrical
engineers almost always calculate the scalar and magnetic potentials
instead of calculating E and B directly.
first citation in article
-
The general argument for the least-action derivation of the field equations comes from L. D. Landau and E. M. Lifschitz, The Classical Theory of Fields (Pergamon, Oxford, 1975), 4th ed., pp. 67–74, and from John David Jackson, Classical Electrodynamics (Wiley, New York, 1999), 3rd ed., Sec. 12.7.
first citation in article
-
Reference 23, Landau and Lifschitz, p. 68.
first citation in article
-
With students who are still becoming familiar with the index notation,
the easiest way to have them work out the implications of the
electromagnetic Lagrangian is for them to write out the implied sums in
the two terms (because the metric is diagonal, there are not that many
terms to write) and then calculate the Euler–Lagrange equation for a
specific field coordinate (say Ax) to see how the calculation goes.
first citation in article
-
Dare A. Wells, Shaum's Outline of Theory and Problems of Lagrangian Dynamics (McGraw–Hill, New York, 1967). The section on electrical and electromechanical systems is Chap. 15.
first citation in article
-
Davison E. Soper, Classical Field Theory (Wiley, New York, 1976).
first citation in article
-
D. A. Van Baak, "Variational alternatives to Kirchoff's loop theorem," Am. J. Phys. 67, 36–44 (1999). [ISI]
first citation in article
-
Charles W. Misner, Kip S. Thorne, and John Archibald Wheeler, Gravitation (Freeman, San Francisco, 1973), Chap. 21.
first citation in article
CITING ARTICLES
This list contains links to other online articles that cite the article currently being viewed.
-
Hamilton's principle: Why is the integrated difference of the kinetic and potential energy minimized?
Alberto G. Rojo, Am. J. Phys. 73, 831 (2005)
FIGURES
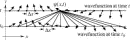 Full figure (9 kB)
Full figure (9 kB)Fig. 1. We can calculate the wave function amplitude 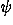 (x,t) at position x at time t by using Eq. (1) to calculate the contribution of the wave function amplitude
(x,t) at position x at time t by using Eq. (1) to calculate the contribution of the wave function amplitude 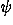 (xi,t0) at a position xi at an earlier time t0 and then summing over all xi. The diagonal lines show the direct paths that connect the various points xi with the final point x. First citation in article
(xi,t0) at a position xi at an earlier time t0 and then summing over all xi. The diagonal lines show the direct paths that connect the various points xi with the final point x. First citation in article
FOOTNOTES
aElectronic mail: tmoore@pomona.edu
Up: Issue Table of Contents
Go to: Previous Article | Next Article
Other formats: HTML (smaller files) | PDF (86 kB)
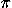 with the arrow contributed by the world line of least action; neither the length nor the direction of the sum is much affected if one ignores all other paths. Indeed, one finds that for a free particle, the direction (in the complex plane) of the arrow representing the sum at b is always rotated by 45° relative to the direction of the arrow contributed by the least-action world line at b (which in turn is simply a rotated version of the arrow at the initial event a), and the sum's magnitude depends on how far a path must deviate from the least-action world line to yield a contributed arrow that makes an angle of
with the arrow contributed by the world line of least action; neither the length nor the direction of the sum is much affected if one ignores all other paths. Indeed, one finds that for a free particle, the direction (in the complex plane) of the arrow representing the sum at b is always rotated by 45° relative to the direction of the arrow contributed by the least-action world line at b (which in turn is simply a rotated version of the arrow at the initial event a), and the sum's magnitude depends on how far a path must deviate from the least-action world line to yield a contributed arrow that makes an angle of 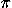 with the least-action arrow.
with the least-action arrow. 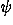 (xi,t0) at various positions xi at some initial time t0. The arrow
(xi,t0) at various positions xi at some initial time t0. The arrow 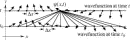 Figure 1.
Figure 1. ![<i>S</i> = –<i>m</i><i>c</i><sup>2</sup>[integral]<i>d</i> <i>tau</i>,](moore_action_files/522_1m0.gif)
![<i>S</i> = –<i>m</i><i>c</i><sup>2</sup>[integral] ((<i>d</i> <i>tau</i>)/<i>d</i><i>t</i>) <i>d</i><i>t</i> = –<i>m</i><i>c</i><sup>2</sup>[integral] sqrt(1–((<i>nu</i><sup>2</sup>)/<i>c</i><sup>2</sup>)) <i>d</i><i>t</i>,](moore_action_files/522_1m1.gif)

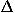 xi around the position xi at an earlier time t0 is given by
xi around the position xi at an earlier time t0 is given by ![<i>K</i>(<i>x</i>,<i>t</i>,<i>x</i><sub><i>i</i></sub>,<i>t</i><sub>0</sub>)<i>psi</i>(<i>x</i><sub><i>i</i></sub>,<i>t</i><sub>0</sub>)<i>Delta</i> <i>x</i><sub><i>i</i></sub> = sqrt((<i>m</i>/(<i>h</i>(<i>t</i> – <i>t</i><sub>0</sub>)<i>i</i>))) <i>e</i><sup><i>i</i><i>S</i><sub>direct</sub>/[h-bar]</sup><i>psi</i>(<i>x</i><sub><i>i</i></sub>,<i>t</i><sub>0</sub>)<i>Delta</i> <i>x</i><sub><i>i</i></sub>,](moore_action_files/522_1m3.gif)
![<i>S</i><sub>direct</sub> = (<i>T</i> – <i>V</i>)<i>Delta</i> <i>t</i> = [(1/2) <i>m</i>(((<i>x</i> – <i>x</i><sub><i>i</i></sub>)/(<i>Delta</i> <i>t</i>)))<sup>2</sup> – <i>V</i>]<i>Delta</i> <i>t</i> = ((<i>m</i><i>u</i><sup>2</sup>)/(2 <i>Delta</i> <i>t</i>)) – <i>V</i> <i>Delta</i> <i>t</i>,](moore_action_files/522_1m4.gif)
![[equivalent]](moore_action_files/equiv.gif) t–t0 is the (coordinate) time difference between the events and u
t–t0 is the (coordinate) time difference between the events and u![<i>K</i>(<i>x</i>,<i>t</i>,<i>x</i><sub><i>i</i></sub>,<i>t</i><sub>0</sub>) = sqrt((<i>m</i>/(<i>h</i>(<i>t</i> – <i>t</i><sub>0</sub>)<i>i</i>))) exp(((<i>i</i><i>m</i><i>u</i><sup>2</sup>)/(2[h-bar] <i>Delta</i> <i>t</i>)))exp(–((<i>i</i> <i>Delta</i> <i>t</i>)/([h-bar])) <i>V</i>).](moore_action_files/522_1m5.gif)
![((<i>m</i><i>u</i><sup>2</sup>)/(2[h-bar] <i>Delta</i> <i>t</i>)) < <i>pi</i> or <i>u</i><sup>2</sup> < (<i>h</i>/<i>m</i>) <i>Delta</i> <i>t</i>.](moore_action_files/522_1m6.gif)
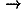 0. The sum over all xi in this limit therefore becomes
0. The sum over all xi in this limit therefore becomes ![<i>psi</i>(<i>x</i>,<i>t</i>) = sqrt((<i>m</i>/(<i>i</i><i>h</i> <i>Delta</i> <i>t</i>))) [integral]<sub>–[infinity]</sub><sup>[infinity]</sup> exp(((<i>i</i><i>m</i><i>u</i><sup>2</sup>)/(2[h-bar] <i>Delta</i> <i>t</i>)))exp(–((<i>i</i> <i>Delta</i> <i>t</i>)/([h-bar])) <i>V</i>(<i>x</i>))<i>psi</i>(<i>x</i> + <i>u</i>,<i>t</i><sub>0</sub>)<i>d</i><i>u</i>,](moore_action_files/522_1m7.gif)
![[integral]](moore_action_files/int.gif)
![<sub>–[infinity]</sub><sup>[infinity]</sup>](moore_action_files/522_1m8.gif) une–au2du,
une–au2du,![<i>psi</i>(<i>x</i>,<i>t</i>) = <i>psi</i>(<i>x</i>,<i>t</i><sub>0</sub>) + 0–(([h-bar] <i>Delta</i> <i>t</i>)/2<i>i</i><i>m</i>) (([partial-derivative]<sup>2</sup><i>psi</i>)/([partial-derivative]<i>x</i><sup>2</sup>))–((<i>i</i> <i>Delta</i> <i>t</i>)/([h-bar])) <i>V</i>(<i>x</i>)<i>psi</i>(<i>x</i>,<i>t</i><sub>0</sub>).](moore_action_files/522_1m9.gif)
![[h-bar]](moore_action_files/planck.gif) /
/
![<i>F</i><sup><i>µ</i> <i>nu</i></sup> = [(0, – <i>E</i><sub><i>x</i></sub>, – <i>E</i><sub><i>y</i></sub>, – <i>E</i><sub><i>z</i></sub>; <i>E</i><sub><i>x</i></sub>, 0, – <i>B</i><sub><i>z</i></sub>, <i>B</i><sub><i>y</i></sub>; <i>E</i><sub><i>y</i></sub>, <i>B</i><sub><i>z</i></sub>, 0, – <i>B</i><sub><i>x</i></sub>; <i>E</i><sub><i>z</i></sub>, – <i>B</i><sub><i>y</i></sub>, <i>B</i><sub><i>x</i></sub>, 0)],](moore_action_files/522_1m11.gif)
 is the charged particle's four-velocity with components ut = [1–
is the charged particle's four-velocity with components ut = [1–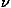 2/c2]–1/2
2/c2]–1/2 , ui =
, ui = 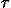 is the proper time measured along its world line and I am using a metric with a timelike signature (+–––). Equation (
is the proper time measured along its world line and I am using a metric with a timelike signature (+–––). Equation (<i>d</i><i>t</i> = [integral]((1/2) <i>m</i> <i>nu</i><sup>2</sup> – <i>q</i> <i>phi</i>)<i>d</i><i>t</i>.](moore_action_files/522_1m12.gif)
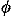 a relativistic scalar or something else? By considering the field between the plates of a parallel-plate capacitor when viewed in a frame moving parallel to the plates, it can be quickly argued that
a relativistic scalar or something else? By considering the field between the plates of a parallel-plate capacitor when viewed in a frame moving parallel to the plates, it can be quickly argued that <i>d</i> <i>tau</i> = –[integral](<i>m</i><i>c</i><sup>2</sup> + <i>q</i><i>u</i><sub><i>µ</i></sub><i>A</i><sup><i>µ</i></sup>) ((<i>d</i> <i>tau</i>)/<i>d</i><i>t</i>) <i>d</i><i>t</i>](moore_action_files/522_1m13.gif)
/<i>c</i><sup>2</sup>)) – <i>q</i> <i>phi</i> +(<i>q</i>/<i>c</i>) <b>v · A</b>)<i>d</i><i>t</i>,](moore_action_files/522_1m14.gif)
![(([partial-derivative]<i>L</i>)/([partial-derivative]<i>x</i>)) = –<i>q</i> (([partial-derivative] <i>phi</i>)/([partial-derivative]<i>x</i>))+(<i>q</i>/<i>c</i>) (<i>nu</i><sup><i>x</i></sup> (([partial-derivative]<i>A</i><sup><i>x</i></sup>)/([partial-derivative]<i>x</i>)) + <i>nu</i><sup><i>y</i></sup> (([partial-derivative]<i>A</i><sup><i>y</i></sup>)/([partial-derivative]<i>x</i>)) + <i>nu</i><sup><i>z</i></sup> (([partial-derivative]<i>A</i><sup><i>z</i></sup>)/([partial-derivative]<i>x</i>))),](moore_action_files/522_1m15.gif)
![(([partial-derivative]<i>L</i>)/([partial-derivative] <i>nu</i><sup><i>x</i></sup>)) = ((<i>m</i> <i>nu</i><sup><i>x</i></sup>)/(sqrt(1 – <i>nu</i><sup>2</sup>/<i>c</i><sup>2</sup>)))+(<i>q</i>/<i>c</i>) <i>A</i><sup><i>x</i></sup> = <i>p</i><sup><i>x</i></sup>+(<i>q</i>/<i>c</i>) <i>A</i><sup><i>x</i></sup>,](moore_action_files/522_1m16.gif)
![((<i>d</i><i>p</i><sup><i>x</i></sup>)/<i>d</i><i>t</i>)+(<i>q</i>/<i>c</i>) ((([partial-derivative]<i>A</i><sup><i>x</i></sup>)/([partial-derivative]<i>t</i>))+(([partial-derivative]<i>A</i><sup><i>x</i></sup>)/([partial-derivative]<i>x</i>)) <i>nu</i><sup><i>x</i></sup>+(([partial-derivative]<i>A</i><sup><i>x</i></sup>)/([partial-derivative]<i>y</i>)) <i>nu</i><sup><i>y</i></sup>+(([partial-derivative]<i>A</i><sup><i>x</i></sup>)/([partial-derivative]<i>z</i>)) <i>nu</i><sup><i>z</i></sup>) = –<i>q</i> (([partial-derivative] <i>phi</i>)/([partial-derivative]<i>x</i>))+(<i>q</i>/<i>c</i>) (<i>nu</i><sup><i>x</i></sup> (([partial-derivative]<i>A</i><sup><i>x</i></sup>)/([partial-derivative]<i>x</i>)) + <i>nu</i><sup><i>y</i></sup> (([partial-derivative]<i>A</i><sup><i>y</i></sup>)/([partial-derivative]<i>x</i>)) + <i>nu</i><sup><i>z</i></sup> (([partial-derivative]<i>A</i><sup><i>z</i></sup>)/([partial-derivative]<i>x</i>))),](moore_action_files/522_1m17.gif)
![((<i>d</i><i>p</i><sup><i>x</i></sup>)/<i>d</i><i>t</i>) = –<i>q</i> (([partial-derivative] <i>phi</i>)/([partial-derivative]<i>x</i>))–(<i>q</i>/<i>c</i>) (([partial-derivative]<i>A</i><sup><i>x</i></sup>)/([partial-derivative]<i>t</i>))+(<i>q</i>/<i>c</i>) <i>nu</i><sup><i>y</i></sup>((([partial-derivative]<i>A</i><sup><i>y</i></sup>)/([partial-derivative]<i>x</i>))–(([partial-derivative]<i>A</i><sup><i>x</i></sup>)/([partial-derivative]<i>y</i>)))–(<i>q</i>/<i>c</i>) <i>nu</i><sup><i>z</i></sup> ((([partial-derivative]<i>A</i><sup><i>x</i></sup>)/([partial-derivative]<i>z</i>))–(([partial-derivative]<i>A</i><sup><i>z</i></sup>)/([partial-derivative]<i>x</i>))).](moore_action_files/522_1m18.gif)
![<i>E</i><sup><i>x</i></sup> = –(1/<i>c</i>) (([partial-derivative]<i>A</i><sup><i>x</i></sup>)/([partial-derivative]<i>t</i>))–(([partial-derivative] <i>phi</i>)/([partial-derivative]<i>x</i>)).](moore_action_files/522_1m19.gif)
![<b>B</b> = [del] × <b>A</b>,](moore_action_files/522_1m20.gif)
![<i>F</i><sup><i>µ</i> <i>nu</i></sup> = [partial-derivative]<sup><i>µ</i></sup><i>A</i><sup><i>nu</i></sup> – [partial-derivative]<sup><i>nu</i></sup><i>A</i><sup><i>µ</i></sup>,](moore_action_files/522_1m21.gif)
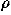 ,j/c], where j is the ordinary current density, so that the sources will appear linearly in the field equation. The only plausible term with the right units in this case is AµJµ. Therefore, the least-action principle for the electromagnetic field must be something like
,j/c], where j is the ordinary current density, so that the sources will appear linearly in the field equation. The only plausible term with the right units in this case is AµJµ. Therefore, the least-action principle for the electromagnetic field must be something like  <i>F</i><sub><i>µ</i> <i>nu</i></sub><i>F</i><sup><i>µ</i> <i>nu</i></sup> + <i>b</i><i>A</i><sub><i>µ</i></sub><i>J</i><sup><i>µ</i></sup>)<i>d</i><i>t</i> <i>d</i><i>x</i> <i>d</i><i>y</i> <i>d</i><i>z</i> = [integral](–(1/<i>k</i>) [<i>g</i><sup><i>µ</i> <i>alpha</i></sup><i>g</i><sup><i>nu</i> <i>beta</i></sup>([partial-derivative]<sub><i>µ</i></sub><i>A</i><sub><i>nu</i></sub> – [partial-derivative]<sub><i>nu</i></sub><i>A</i><sub><i>µ</i></sub>)([partial-derivative]<sub><i>alpha</i></sub><i>A</i><sub><i>beta</i></sub> – [partial-derivative]<sub><i>beta</i></sub><i>A</i><sub><i>alpha</i></sub>)] + <i>b</i><i>A</i><sub><i>µ</i></sub><i>J</i><sup><i>µ</i></sup>)<i>d</i><i>t</i> <i>d</i><i>x</i> <i>d</i><i>y</i> <i>d</i><i>z</i>,](moore_action_files/522_1m22.gif)
 is the inverse flat-space metric and b is some unitless constant that specifies the relative magnitude and sign of the two terms. The field quantities Aµ play the role of coordinates and the gradients
is the inverse flat-space metric and b is some unitless constant that specifies the relative magnitude and sign of the two terms. The field quantities Aµ play the role of coordinates and the gradients ![[partial-derivative]](moore_action_files/part.gif) µA
µA![[partial-derivative]<sub><i>µ</i></sub>([partial-derivative]<sub><i>µ</i></sub><i>A</i><sup><i>nu</i></sup> – [partial-derivative]<sup><i>nu</i></sup><i>A</i><sup><i>µ</i></sup>) = [partial-derivative]<sub><i>µ</i></sub><i>F</i><sup><i>µ</i> <i>nu</i></sup> = –(<i>b</i><i>k</i>/4) <i>J</i><sup><i>nu</i></sup>.](moore_action_files/522_1m23.gif)
 www.eftaylor.com/leastaction.html
www.eftaylor.com/leastaction.html .
.