American Journal of Physics, Vol. 72, No. 4, pp. 510–513, April 2004
©2004 American Association of Physics Teachers. All rights reserved.
Deriving Lagrange's equations using elementary calculus
Jozef Hanca)
Technical University, Vysokoskolska 4, 042 00 Kosice, Slovakia
Edwin F. Taylorb)
Massachusetts Institute of Technology, Cambridge, Massachusetts 02139
Slavomir Tulejac)
Gymnazium arm. gen. L. Svobodu, Komenskeho 4, 066 51 Humenne, Slovakia
Received: 30 December 2002; accepted: 20 June 2003We derive Lagrange's equations of motion from the principle of least action using elementary calculus rather than the calculus of variations. We also demonstrate the conditions under which energy and momentum are constants of the motion. © 2004 American Association of Physics Teachers.
Contents
I. INTRODUCTION
The equations of motion1 of a mechanical system can be derived by two different mathematical methods—vectorial and analytical. Traditionally, introductory mechanics begins with Newton's laws of motion which relate the force, momentum, and acceleration vectors. But we frequently need to describe systems, for example, systems subject to constraints without friction, for which the use of vector forces is cumbersome. Analytical mechanics in the form of the Lagrange equations provides an alternative and very powerful tool for obtaining the equations of motion. Lagrange's equations employ a single scalar function, and there are no annoying vector components or associated trigonometric manipulations. Moreover, the analytical approach using Lagrange's equations provides other capabilities2 that allow us to analyze a wider range of systems than Newton's second law.
The derivation of Lagrange's equations in advanced mechanics texts3 typically applies the calculus of variations to the principle of least action. The calculus of variation belongs to important branches of mathematics, but is not widely taught or used at the college level. Students often encounter the variational calculus first in an advanced mechanics class, where they struggle to apply a new mathematical procedure to a new physical concept. This paper provides a derivation of Lagrange's equations from the principle of least action using elementary calculus,4 which may be employed as an alternative to (or a preview of) the more advanced variational calculus derivation.
In Sec. II we develop the mathematical background for deriving Lagrange's equations from elementary calculus. Section III gives the derivation of the equations of motion for a single particle. Section IV extends our approach to demonstrate that the energy and momentum are constants of the motion. The Appendix expands Lagrange's equations to multiparticle systems and adds angular momentum as an example of generalized momentum.
II. DIFFERENTIAL APPROXIMATION TO THE PRINCIPLE OF LEAST ACTION
A particle moves along the x axis with potential energy V(x) which is time independent. For this special case the Lagrange function or Lagrangian L has the form:5
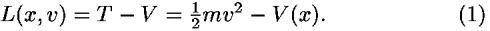
The action S along a world line is defined as
![<i>S</i> = [integral]<sub>(along the; world line; )</sub> <i>L</i>(<i>x</i>,<i>v</i>)<i>d</i><i>t</i>.](lagrange_files/510_1m1.gif)
The principle of least action requires that between a fixed initial event and a fixed final event the particle follow a world line such that the action S is a minimum.
The action S is an additive scalar quantity, and is the sum of contributions L t from each segment along the entire world line between two events fixed in space and time. Because S is additive, it follows that the principle of least action must hold for each individual infinitesimal segment of the world line.6 This property allows us to pass from the integral equation for the principle of least action, Eq. (2), to Lagrange's differential equation, valid anywhere along the world line. It also allows us to use elementary calculus in this derivation.
t from each segment along the entire world line between two events fixed in space and time. Because S is additive, it follows that the principle of least action must hold for each individual infinitesimal segment of the world line.6 This property allows us to pass from the integral equation for the principle of least action, Eq. (2), to Lagrange's differential equation, valid anywhere along the world line. It also allows us to use elementary calculus in this derivation.
We approximate a small section of the world line by two straight-line segments connected in the middle (Fig. 1) and make the following approximations: The average position coordinate in the Lagrangian along a segment is at the midpoint of the segment.7 The average velocity of the particle is equal to its displacement across the segment divided by the time interval of the segment. These approximations applied to segment A in Fig. 1 yield the average Lagrangian LA and action SA contributed by this segment:
![<i>L</i><sub><i>A</i></sub> [equivalent] <i>L</i>(((<i>x</i><sub>1</sub> + <i>x</i><sub>2</sub>)/2),((<i>x</i><sub>2</sub> – <i>x</i><sub>1</sub>)/(<i>Delta</i> <i>t</i>))),](lagrange_files/510_1m2.gif)
![<i>S</i><sub><i>A</i></sub> [approximate] <i>L</i><sub><i>A</i></sub><i>Delta</i> <i>t</i> = <i>L</i>(((<i>x</i><sub>1</sub> + <i>x</i><sub>2</sub>)/2),((<i>x</i><sub>2</sub> – <i>x</i><sub>1</sub>)/(<i>Delta</i> <i>t</i>)))<i>Delta</i> <i>t</i>,](lagrange_files/510_1m3.gif)
with similar expressions for LB and SB along segment B.
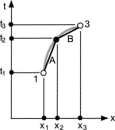 Figure 1.
Figure 1. III. DERIVATION OF LAGRANGE'S EQUATION
We employ the approximations of Sec. II to derive Lagrange's equations for the special case introduced there. As shown in Fig. 2, we fix events 1 and 3 and vary the x coordinate of the intermediate event to minimize the action between the outer two events.
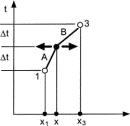 Figure 2.
Figure 2. For simplicity, but without loss of generality, we choose the time increment 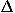 t to be the same for each segment, which also equals the time between the midpoints of the two segments. The average positions and velocities along segments A and B are
t to be the same for each segment, which also equals the time between the midpoints of the two segments. The average positions and velocities along segments A and B are

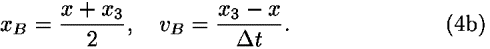
The expressions in Eq. (4) are all functions of the single variable x. For later use we take the derivatives of Eq. (4) with respect to x:
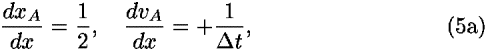
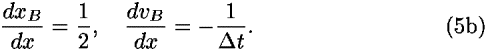
Let LA and LB be the values of the Lagrangian on segments A and B, respectively, using Eq. (4), and label the summed action across these two segments as SAB:

The principle of least action requires that the coordinates of the middle event x be chosen to yield the smallest value of the action between the fixed events 1 and 3. If we set the derivative of SAB with respect to x equal to zero8 and use the chain rule, we obtain
![((<i>d</i><i>S</i><sub><i>A</i><i>B</i></sub>)/<i>d</i><i>x</i>) = 0 = (([partial-derivative]<i>L</i><sub><i>A</i></sub>)/([partial-derivative]<i>x</i><sub><i>A</i></sub>)) ((<i>d</i><i>x</i><sub><i>A</i></sub>)/<i>d</i><i>x</i>) <i>Delta</i> <i>t</i>+(([partial-derivative]<i>L</i><sub><i>A</i></sub>)/([partial-derivative]<i>v</i><sub><i>A</i></sub>)) ((<i>d</i><i>v</i><sub><i>A</i></sub>)/<i>d</i><i>x</i>) <i>Delta</i> <i>t</i>+(([partial-derivative]<i>L</i><sub><i>B</i></sub>)/([partial-derivative]<i>x</i><sub><i>B</i></sub>)) ((<i>d</i><i>x</i><sub><i>B</i></sub>)/<i>d</i><i>x</i>) <i>Delta</i> <i>t</i>+(([partial-derivative]<i>L</i><sub><i>B</i></sub>)/([partial-derivative]<i>v</i><sub><i>B</i></sub>)) ((<i>d</i><i>v</i><sub><i>B</i></sub>)/<i>d</i><i>x</i>) <i>Delta</i> <i>t</i>.](lagrange_files/510_1m9.gif)
We substitute Eq. (5) into Eq. (7), divide through by 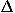 t, and regroup the terms to obtain
t, and regroup the terms to obtain
![(1/2) ((([partial-derivative]<i>L</i><sub><i>A</i></sub>)/([partial-derivative]<i>x</i><sub><i>A</i></sub>))+(([partial-derivative]<i>L</i><sub><i>B</i></sub>)/([partial-derivative]<i>x</i><sub><i>B</i></sub>)))–(1/(<i>Delta</i> <i>t</i>)) ((([partial-derivative]<i>L</i><sub><i>B</i></sub>)/([partial-derivative]<i>v</i><sub><i>B</i></sub>))–(([partial-derivative]<i>L</i><sub><i>A</i></sub>)/([partial-derivative]<i>v</i><sub><i>A</i></sub>))) = 0.](lagrange_files/510_1m10.gif)
To first order, the first term in Eq. (8) is the average value of ![[partial-derivative]](lagrange_files/part.gif) L/
L/![[partial-derivative]](lagrange_files/part.gif) x on the two segments A and B. In the limit
x on the two segments A and B. In the limit 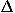 t
t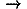 0, this term approaches the value of the partial derivative at x. In the same limit, the second term in Eq. (8) becomes the time derivative of the partial derivative of the Lagrangian with respect to velocity d(
0, this term approaches the value of the partial derivative at x. In the same limit, the second term in Eq. (8) becomes the time derivative of the partial derivative of the Lagrangian with respect to velocity d(![[partial-derivative]](lagrange_files/part.gif) L/
L/![[partial-derivative]](lagrange_files/part.gif) v)/dt. Therefore in the limit
v)/dt. Therefore in the limit  t
t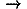 0, Eq. (8) becomes the Lagrange equation in x:
0, Eq. (8) becomes the Lagrange equation in x:
![(([partial-derivative]<i>L</i>)/([partial-derivative]<i>x</i>))–(<i>d</i>/<i>d</i><i>t</i>) ((([partial-derivative]<i>L</i>)/([partial-derivative]<i>v</i>))) = 0.](lagrange_files/510_1m11.gif)
We did not specify the location of segments A and B along the world line. The additive property of the action implies that Eq. (9) is valid for every adjacent pair of segments.
An essentially identical derivation applies to any particle with one degree of freedom in any potential. For example, the single angle 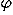 tracks the motion of a simple pendulum, so its equation of motion follows from Eq. (9) by replacing x with
tracks the motion of a simple pendulum, so its equation of motion follows from Eq. (9) by replacing x with 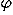 without the need to take vector components.
without the need to take vector components.
IV. MOMENTUM AND ENERGY AS CONSTANTS OF THE MOTION
A. Momentum
We consider the case in which the Lagrangian does not depend explicitly on the x coordinate of the particle (for example, the potential is zero or independent of position). Because it does not appear in the Lagrangian, the x coordinate is "ignorable" or "cyclic." In this case a simple and well-known conclusion from Lagrange's equation leads to the momentum as a conserved quantity, that is, a constant of motion. Here we provide an outline of the derivation.
For a Lagrangian that is only a function of the velocity, L = L(v), Lagrange's equation (9) tells us that the time derivative of ![[partial-derivative]](lagrange_files/part.gif) L/
L/![[partial-derivative]](lagrange_files/part.gif) v is zero. From Eq. (1), we find that
v is zero. From Eq. (1), we find that ![[partial-derivative]](lagrange_files/part.gif) L/
L/![[partial-derivative]](lagrange_files/part.gif) v = mv, which implies that the x momentum, p = mv, is a constant of the motion.
v = mv, which implies that the x momentum, p = mv, is a constant of the motion.
This usual consideration can be supplemented or replaced by our approach. If we repeat the derivation in Sec. III with L = L(v) (perhaps as a student exercise to reinforce understanding of the previous derivation), we obtain from the principle of least action
![((<i>d</i><i>S</i><sub><i>A</i><i>B</i></sub>)/<i>d</i><i>x</i>) = 0 = (([partial-derivative]<i>L</i><sub><i>A</i></sub>)/([partial-derivative]<i>v</i><sub><i>A</i></sub>)) ((<i>d</i><i>v</i><sub><i>A</i></sub>)/<i>d</i><i>x</i>) <i>Delta</i> <i>t</i>+(([partial-derivative]<i>L</i><sub><i>B</i></sub>)/([partial-derivative]<i>v</i><sub><i>B</i></sub>)) ((<i>d</i><i>v</i><sub><i>B</i></sub>)/<i>d</i><i>x</i>) <i>Delta</i> <i>t</i>.](lagrange_files/510_1m12.gif)
We substitute Eq. (5) into Eq. (10) and rearrange the terms to find:
![(([partial-derivative]<i>L</i><sub><i>A</i></sub>)/([partial-derivative]<i>v</i><sub><i>A</i></sub>)) = (([partial-derivative]<i>L</i><sub><i>B</i></sub>)/([partial-derivative]<i>v</i><sub><i>B</i></sub>))](lagrange_files/510_1m13.gif)
or

Again we can use the arbitrary location of segments A and B along the world line to conclude that the momentum p is a constant of the motion everywhere on the world line.
B. Energy
Standard texts9 obtain conservation of energy by examining the time derivative of a Lagrangian that does not depend explicitly on time. As pointed out in Ref. 9, this lack of dependence of the Lagrangian implies the homogeneity of time: temporal translation has no influence on the form of the Lagrangian. Thus conservation of energy is closely connected to the symmetry properties of nature.10 As we will see, our elementary calculus approach offers an alternative way11 to derive energy conservation.
Consider a particle in a time-independent potential V(x). Now we vary the time of the middle event (Fig. 3), rather than its position, requiring that this time be chosen to minimize the action.
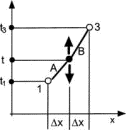 Figure 3.
Figure 3. For simplicity, we choose the x increments to be equal, with the value 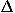 x. We keep the spatial coordinates of all three events fixed while varying the time coordinate of the middle event and obtain
x. We keep the spatial coordinates of all three events fixed while varying the time coordinate of the middle event and obtain
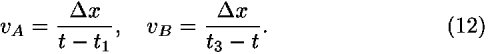
These expressions are functions of the single variable t, with respect to which we take the derivatives
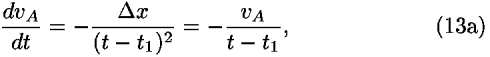
and

Despite the form of Eq. (13), the derivatives of velocities are not accelerations, because the x separations are held constant while the time is varied.
As before [see Eq. (6)],
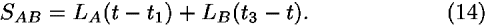
Note that students sometimes misinterpret the time differences in parentheses in Eq. (14) as arguments of L.
We find the value of the time t for the action to be a minimum by setting the derivative of SAB equal to zero:
![((<i>d</i><i>S</i><sub><i>A</i><i>B</i></sub>)/<i>d</i><i>t</i>) = 0 = (([partial-derivative]<i>L</i><sub><i>A</i></sub>)/([partial-derivative]<i>v</i><sub><i>A</i></sub>)) ((<i>d</i><i>v</i><sub><i>A</i></sub>)/<i>d</i><i>t</i>) (<i>t</i> – <i>t</i><sub>1</sub>) + <i>L</i><sub><i>A</i></sub>+(([partial-derivative]<i>L</i><sub><i>B</i></sub>)/([partial-derivative]<i>v</i><sub><i>B</i></sub>)) ((<i>d</i><i>v</i><sub><i>B</i></sub>)/<i>d</i><i>t</i>) (<i>t</i><sub>3</sub> – <i>t</i>) – <i>L</i><sub><i>B</i></sub>.](lagrange_files/510_1m19.gif)
If we substitute Eq. (13) into Eq. (15) and rearrange the result, we find
![(([partial-derivative]<i>L</i><sub><i>A</i></sub>)/([partial-derivative]<i>v</i><sub><i>A</i></sub>)) <i>v</i><sub><i>A</i></sub> – <i>L</i><sub><i>A</i></sub> = (([partial-derivative]<i>L</i><sub><i>B</i></sub>)/([partial-derivative]<i>v</i><sub><i>B</i></sub>)) <i>v</i><sub><i>B</i></sub> – <i>L</i><sub><i>B</i></sub>.](lagrange_files/510_1m20.gif)
Because the action is additive, Eq. (16) is valid for every segment of the world line and identifies the function v![[partial-derivative]](lagrange_files/part.gif) L/
L/![[partial-derivative]](lagrange_files/part.gif) v–L as a constant of the motion. By substituting Eq. (1) for the Lagrangian into v
v–L as a constant of the motion. By substituting Eq. (1) for the Lagrangian into v![[partial-derivative]](lagrange_files/part.gif) L/
L/![[partial-derivative]](lagrange_files/part.gif) v–L and carrying out the partial derivatives, we can show that the constant of the motion corresponds to the total energy E = T + V.
v–L and carrying out the partial derivatives, we can show that the constant of the motion corresponds to the total energy E = T + V.
V. SUMMARY
Our derivation and the extension to multiple degrees of freedom in the Appendix allow the introduction of Lagrange's equations and its connection to the principle of least action without the apparatus of the calculus of variations. The derivations also may be employed as a preview of Lagrangian mechanics before its more formal derivation using variational calculus.
One of us (ST) has successfully employed these derivations and the resulting Lagrange equations with a small group of talented high school students. They used the equations to solve problems presented in the Physics Olympiad. The excitement and enthusiasm of these students leads us to hope that others will undertake trials with larger numbers and a greater variety of students.
ACKNOWLEDGMENT
The authors would like to express thanks to an anonymous referee for his or her valuable criticisms and suggestions, which improved this paper.
APPENDIX: EXTENSION TO MULTIPLE DEGREES OF FREEDOM
We discuss Lagrange's equations for a system with multiple degrees of freedom, without pausing to discuss the usual conditions assumed in the derivations, because these can be found in standard advanced mechanics texts.3
Consider a mechanical system described by the following Lagrangian:
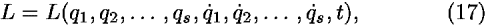
where the q are independent generalized coordinates and the dot over q indicates a derivative with respect to time. The subscript s indicates the number of degrees of freedom of the system. Note that we have generalized to a Lagrangian that is an explicit function of time t. The specification of all the values of all the generalized coordinates qi in Eq. (17) defines a configuration of the system. The action S summarizes the evolution of the system as a whole from an initial configuration to a final configuration, along what might be called a world line through multidimensional space–time. Symbolically we write:
![<i>S</i> = [integral]<sub>(initial configuration; to final configuration; )</sub> <i>L</i>(<i>q</i><sub>1</sub>,<i>q</i><sub>2</sub>...<i>q</i><sub><i>s</i></sub>,<i>q</i>-dot<sub>1</sub>,<i>q</i>-dot<sub>2</sub>...<i>q</i>-dot<sub><i>s</i></sub>,<i>t</i>)<i>d</i><i>t</i>.](lagrange_files/510_1m22.gif)
The generalized principle of least action requires that the value of S be a minimum for the actual evolution of the system symbolized in Eq. (18). We make an argument similar to that in Sec. III for the one-dimensional motion of a particle in a potential. If the principle of least action holds for the entire world line through the intermediate configurations of L in Eq. (18), it also holds for an infinitesimal change in configuration anywhere on this world line.
Let the system pass through three infinitesimally close configurations in the ordered sequence 1, 2, 3 such that all generalized coordinates remain fixed except for a single coordinate q at configuration 2. Then the increment of the action from configuration 1 to configuration 3 can be considered to be a function of the single variable q. As a consequence, for each of the s degrees of freedom, we can make an argument formally identical to that carried out from Eq. (3) through Eq. (9). Repeated s times, once for each generalized coordinate qi, this derivation leads to s scalar Lagrange equations that describe the motion of the system:
![(([partial-derivative]<i>L</i>)/([partial-derivative]<i>q</i><sub><i>i</i></sub>))–(<i>d</i>/<i>d</i><i>t</i>) ((([partial-derivative]<i>L</i>)/([partial-derivative]<i>q</i>-dot<sub><i>i</i></sub>))) = 0 (<i>i</i> = 1,2,3,...,<i>s</i>).](lagrange_files/510_1m23.gif)
The inclusion of time explicitly in the Lagrangian (17) does not affect these derivations, because the time coordinate is held fixed in each equation.
Suppose that the Lagrangian (17) is not a function of a given coordinate qk. An argument similar to that in Sec. IV A tells us that the corresponding generalized momentum ![[partial-derivative]](lagrange_files/part.gif) L/
L/![[partial-derivative]](lagrange_files/part.gif)
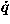 k is a constant of the motion. As a simple example of such a generalized momentum, we consider the angular momentum of a particle in a central potential. If we use polar coordinates r,
k is a constant of the motion. As a simple example of such a generalized momentum, we consider the angular momentum of a particle in a central potential. If we use polar coordinates r,  to describe the motion of a single particle in the plane, then the Lagrangian has the form L = T–V = m(
to describe the motion of a single particle in the plane, then the Lagrangian has the form L = T–V = m(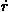 2 + r2
2 + r2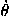 2)/2–V(r), and the angular momentum of the system is represented by
2)/2–V(r), and the angular momentum of the system is represented by ![[partial-derivative]](lagrange_files/part.gif) L/
L/![[partial-derivative]](lagrange_files/part.gif)
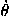 .
.
If the Lagrangian (17) is not an explicit function of time, then a derivation formally equivalent to that in Sec. IVB (with time as the single variable) shows that the function (![[summation]](lagrange_files/sum.gif)
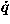 1
1![[partial-derivative]](lagrange_files/part.gif) L/
L/![[partial-derivative]](lagrange_files/part.gif)
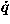 i)–L, sometimes called12 the energy function h, is a constant of the motion of the system, which in the simple cases we cover13 can be interpreted as the total energy E of the system.
i)–L, sometimes called12 the energy function h, is a constant of the motion of the system, which in the simple cases we cover13 can be interpreted as the total energy E of the system.
If the Lagrangian (17) depends explicitly on time, then this derivation yields the equation dh/dt = –![[partial-derivative]](lagrange_files/part.gif) L/
L/![[partial-derivative]](lagrange_files/part.gif) t.
t.
REFERENCES
Citation links [e.g., Phys. Rev. D 40, 2172 (1989)] go to online journal abstracts. Other links (see Reference Information) are available with your current login. Navigation of links may be more efficient using a second browser window.
-
We take "equations of motion" to mean relations between the
accelerations, velocities, and coordinates of a mechanical system. See
L. D. Landau and E. M. Lifshitz, Mechanics (Butterworth-Heinemann, Oxford, 1976), Chap. 1, Sec. 1.
first citation in article
-
Besides its expression in scalar quantities (such as kinetic and
potential energy), Lagrangian quantities lead to the reduction of
dimensionality of a problem, employ the invariance of the equations
under point transformations, and lead directly to constants of the
motion using Noether's theorem. More detailed explanation of these
features, with a comparison of analytical mechanics to vectorial
mechanics, can be found in Cornelius Lanczos, The Variational Principles of Mechanics (Dover, New York, 1986), pp. xxi–xxix.
first citation in article
-
Chapter 1 in Ref. 1 and Chap. V in Ref. 2; Gerald J. Sussman and Jack Wisdom, Structure and Interpretation of Classical Mechanics (MIT, Cambridge, 2001), Chap. 1; Herbert Goldstein, Charles Poole, and John Safko, Classical Mechanics
(Addison–Wesley, Reading, MA, 2002), 3rd ed., Chap. 2. An alternative
method derives Lagrange's equations from D'Alambert principle; see
Goldstein, Sec. 1.4. first citation in article
-
Our derivation is a modification of the finite difference technique
employed by Euler in his path-breaking 1744 work, "The method of
finding plane curves that show some property of maximum and minimum."
Complete references and a description of Euler's original treatment can
be found in Herman H. Goldstine, A History of the Calculus of Variations from the 17th Through the 19th Century
(Springer-Verlag, New York, 1980), Chap. 2. Cornelius Lanczos (Ref. 2,
pp. 49–54) presents an abbreviated version of Euler's original
derivation using contemporary mathematical notation. first citation in article
-
R. P. Feynman, R. B. Leighton, and M. Sands, The Feynman Lectures on Physics (Addison–Wesley, Reading, MA, 1964), Vol. 2, Chap. 19.
first citation in article
-
See Ref. 5, p. 19-8 or in more detail,
J. Hanc, S. Tuleja, and M. Hancova, "Simple derivation of Newtonian mechanics from the principle of least action," Am. J. Phys. 71 (4), 386–391 (2003). [ISI]
first citation in article
-
There is no particular reason to use the midpoint of the segment in the
Lagrangian of Eq. (2). In Riemann integrals we can use any point on the
given segment. For example, all our results will be the same if we used
the coordinates of either end of each segment instead of the
coordinates of the midpoint. The repositioning of this point can be the
basis of an exercise to test student understanding of the derivations
given here. first citation in article
-
A zero value of the derivative most often leads to the world line of
minimum action. It is possible also to have a zero derivative at an
inflection point or saddle point in the action (or the multidimensional
equivalent in configuration space). So the most general term for our
basic law is the principle of stationary action. The conditions that
guarantee the existence of a minimum can be found in I. M. Gelfand and
S. V. Fomin, Calculus of Variations (Prentice–Hall, Englewood Cliffs, NJ, 1963).
first citation in article
-
Reference 1, Chap. 2 and Ref. 3, Goldstein et al., Sec. 2.7.
first citation in article
-
The most fundamental justification of conservation laws comes from
symmetry properties of nature as described by Noether's theorem. Hence
energy conservation can be derived from the invariance of the action by
temporal translation and conservation of momentum from invariance under
space translation. See N. C. Bobillo-Ares, "Noether's theorem in
discrete classical mechanics," Am. J. Phys. 56 (2), 174–177 (1988)
or C. M. Giordano and A. R. Plastino, "Noether's theorem, rotating potentials, and Jacobi's integral of motion," ibid. 66 (11), 989–995 (1998).
first citation in article
-
Our approach also can be related to symmetries and Noether's theorem,
which is the main subject of J. Hanc, S. Tuleja, and M. Hancova,
"Symmetries and conservation laws: Consequences of Noether's theorem,"
Am. J. Phys. (to be published). first citation in article
-
Reference 3, Goldstein et al., Sec. 2.7.
first citation in article
-
For the case of generalized coordinates, the energy function h is generally not the same as the total energy. The conditions for conservation of the energy function h are distinct from those that identify h
as the total energy. For a detailed discussion see Ref. 12.
Pedagogically useful comments on a particular example can be found in
A. S. de Castro, "Exploring a rheonomic system," Eur. J. Phys. 21, 23–26 (2000) [Inspec]
and C. Ferrario and A. Passerini, "Comment on Exploring a rheonomic system," ibid. 22, L11–L14 (2001). [Inspec] [ISI]
first citation in article
CITING ARTICLES
This list contains links to other online articles that cite the article currently being viewed.
-
Hamilton's principle: Why is the integrated difference of the kinetic and potential energy minimized?
Alberto G. Rojo, Am. J. Phys. 73, 831 (2005)
FIGURES
 Full figure (5 kB)
Full figure (5 kB)Fig. 1. An infinitesimal section of the world line approximated by two straight line segments. First citation in article
 Full figure (6 kB)
Full figure (6 kB)Fig. 2. Derivation of Lagrange's equations from the principle of least action. Points 1 and 3 are on the true world line. The world line between them is approximated by two straight line segments (as in Fig. 1). The arrows show that the x coordinate of the middle event is varied. All other coordinates are fixed. First citation in article
 Full figure (6 kB)
Full figure (6 kB)Fig. 3. A derivation showing that the energy is a constant of the motion. Points 1 and 3 are on the true world line, which is approximated by two straight line segments (as in Figs. 1 and 2). The arrows show that the t coordinate of the middle event is varied. All other coordinates are fixed. First citation in article
FOOTNOTES
aElectronic mail: jozef.hanc@tuke.sk
bElectronic mail: eftaylor@mit.edu; http://www.eftaylor.com
cElectronic mail: tuleja@stonline.sk
Up: Issue Table of Contents
Go to: Previous Article | Next Article
Other formats: HTML (smaller files) | PDF (83 kB)
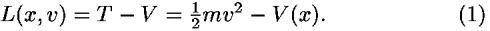
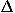 t from each segment along the entire world line between two events fixed in space and time. Because S is additive, it follows that the principle of least action must hold for each individual infinitesimal segment of the world line.6 This property allows us to pass from the integral equation for the principle of least action, Eq. (2), to Lagrange's differential equation, valid anywhere along the world line. It also allows us to use elementary calculus in this derivation.
t from each segment along the entire world line between two events fixed in space and time. Because S is additive, it follows that the principle of least action must hold for each individual infinitesimal segment of the world line.6 This property allows us to pass from the integral equation for the principle of least action, Eq. (2), to Lagrange's differential equation, valid anywhere along the world line. It also allows us to use elementary calculus in this derivation.  Figure 1.
Figure 1.  Figure 2.
Figure 2. 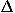 t to be the same for each segment, which also equals the time between the midpoints of the two segments. The average positions and velocities along segments A and B are
t to be the same for each segment, which also equals the time between the midpoints of the two segments. The average positions and velocities along segments A and B are 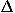 t, and regroup the terms to obtain
t, and regroup the terms to obtain ![[partial-derivative]](lagrange_files/part.gif) L/
L/![[partial-derivative]](lagrange_files/part.gif) x on the two segments A and B. In the limit
x on the two segments A and B. In the limit 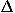 t
t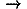 0, this term approaches the value of the partial derivative at x. In the same limit, the second term in Eq. (8) becomes the time derivative of the partial derivative of the Lagrangian with respect to velocity d(
0, this term approaches the value of the partial derivative at x. In the same limit, the second term in Eq. (8) becomes the time derivative of the partial derivative of the Lagrangian with respect to velocity d(![[partial-derivative]](lagrange_files/part.gif) L/
L/![[partial-derivative]](lagrange_files/part.gif) v)/dt. Therefore in the limit
v)/dt. Therefore in the limit 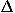 t
t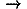 0, Eq. (8) becomes the Lagrange equation in x:
0, Eq. (8) becomes the Lagrange equation in x: 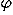 tracks the motion of a simple pendulum, so its equation of motion follows from Eq. (9) by replacing x with
tracks the motion of a simple pendulum, so its equation of motion follows from Eq. (9) by replacing x with 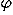 without the need to take vector components.
without the need to take vector components. ![[partial-derivative]](lagrange_files/part.gif) L/
L/![[partial-derivative]](lagrange_files/part.gif) v is zero. From Eq. (1), we find that
v is zero. From Eq. (1), we find that ![[partial-derivative]](lagrange_files/part.gif) L/
L/![[partial-derivative]](lagrange_files/part.gif) v = mv, which implies that the x momentum, p = mv, is a constant of the motion.
v = mv, which implies that the x momentum, p = mv, is a constant of the motion. ![(([partial-derivative]<i>L</i><sub><i>A</i></sub>)/([partial-derivative]<i>v</i><sub><i>A</i></sub>)) = (([partial-derivative]<i>L</i><sub><i>B</i></sub>)/([partial-derivative]<i>v</i><sub><i>B</i></sub>))](lagrange_files/510_1m13.gif)
 Figure 3.
Figure 3. 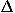 x. We keep the spatial coordinates of all three events fixed while varying the time coordinate of the middle event and obtain
x. We keep the spatial coordinates of all three events fixed while varying the time coordinate of the middle event and obtain ![[partial-derivative]](lagrange_files/part.gif) L/
L/![[partial-derivative]](lagrange_files/part.gif) v–L as a constant of the motion. By substituting Eq. (1) for the Lagrangian into v
v–L as a constant of the motion. By substituting Eq. (1) for the Lagrangian into v![[partial-derivative]](lagrange_files/part.gif) L/
L/![[partial-derivative]](lagrange_files/part.gif) v–L and carrying out the partial derivatives, we can show that the constant of the motion corresponds to the total energy E = T + V.
v–L and carrying out the partial derivatives, we can show that the constant of the motion corresponds to the total energy E = T + V. ![[partial-derivative]](lagrange_files/part.gif) L/
L/![[partial-derivative]](lagrange_files/part.gif)
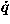 k is a constant of the motion. As a simple example of such a generalized momentum, we consider the angular momentum of a particle in a central potential. If we use polar coordinates r,
k is a constant of the motion. As a simple example of such a generalized momentum, we consider the angular momentum of a particle in a central potential. If we use polar coordinates r,  to describe the motion of a single particle in the plane, then the Lagrangian has the form L = T–V = m(
to describe the motion of a single particle in the plane, then the Lagrangian has the form L = T–V = m(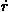 2 + r2
2 + r2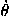 2)/2–V(r), and the angular momentum of the system is represented by
2)/2–V(r), and the angular momentum of the system is represented by ![[partial-derivative]](lagrange_files/part.gif) L/
L/![[partial-derivative]](lagrange_files/part.gif)
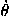 .
. ![[summation]](lagrange_files/sum.gif)
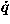 1
1![[partial-derivative]](lagrange_files/part.gif) L/
L/![[partial-derivative]](lagrange_files/part.gif)
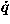 i)–L, sometimes called12 the energy function h, is a constant of the motion of the system, which in the simple cases we cover13 can be interpreted as the total energy E of the system.
i)–L, sometimes called12 the energy function h, is a constant of the motion of the system, which in the simple cases we cover13 can be interpreted as the total energy E of the system. ![[partial-derivative]](lagrange_files/part.gif) L/
L/![[partial-derivative]](lagrange_files/part.gif) t.
t.  Full figure (5 kB)
Full figure (5 kB) Full figure (6 kB)
Full figure (6 kB) Full figure (6 kB)
Full figure (6 kB)